Qué es la jerarquía de operaciones y por qué las personas se confundirían todo el tiempo sin ella

Todos conocemos la jerarquía de las operaciones en matemáticas desde la escuela. Gradualmente olvidamos estas reglas, y debido a esto fácilmente cometemos errores en los cálculos que realizamos en la vida diaria.

Ideas en 5 minutos te explicará qué enseña exactamente la jerarquía de operaciones en matemáticas, por la cual incluso muchos adultos cometen errores en ejercicios “infantiles” y por qué es importante conocerla a cualquier edad.

Por qué se debe seguir el orden correcto de la jerarquía de operaciones

Las operaciones aritméticas básicas en matemáticas son las siguientes:

• Suma (+)
• Resta (-)
• Multiplicación (×)
• División (÷)

Si en la expresión numérica se utiliza solo una operación, no es complicado resolver tal ejercicio. Por ejemplo, 3 + 2 = 5 o 6 ÷ 3 = 2. Cuando hay 2 o más operaciones, para obtener la respuesta correcta se debe emplear la jerarquía de operaciones en el orden correcto.

En la imagen superior hay 3 ejemplos en los cuales es muy fácil equivocarse si se olvida la jerarquía de operaciones en matemáticas. Intenta resolver estos problemas por tu cuenta y después compara el resultado que obtuviste con las respuestas correctas al final del artículo. Si te equivocaste por lo menos en uno, posiblemente debas repetir junto con nosotros las reglas correspondientes a la jerarquía de operaciones.

Regla 1. Las operaciones se resuelven de izquierda a derecha, una a la vez

✅ Al realizar operaciones aritméticas básicas con números, lo habitual es resolverlas de izquierda a derecha.

Presta atención a la imagen superior. Para calcular el resultado de la expresión 6 ÷ 3 × 2, es necesario resolver de forma alternada de izquierda a derecha, primero dividir 6 entre 3 y después multiplicar el resultado por 2. Al realizar la operación en un orden diferente (primero la multiplicación y luego la división), obtendremos una respuesta incorrecta.

❗ Si la expresión consiste solo en operaciones de multiplicación o suma, entonces, de acuerdo con la propiedad conmutativa, el resultado de la expresión no depende de la secuencia en la que se realicen las operaciones.

Regla 2. Primero se hacen la multiplicación y división y solo después la suma y resta

Una expresión puede contener diferentes operaciones aritméticas, como en la imagen superior. Escribimos esto como 2 + 2 × 2. Si realizamos todas las operaciones de izquierda a derecha, obtenemos lo siguiente 2 + 2 × 2 = 4 × 2 = 8. Esta respuesta es incorrecta (puedes comprobarlo contando los cubos de la imagen superior. ¿Por qué pasa esto?

✅ Anteriormente hablamos sobre las 4 operaciones aritméticas básicas. Ellas son desiguales en prioridad, lo cual influye en el orden en que se deben resolver. La multiplicación y división tienen una mayor prioridad, en comparación con la suma y resta. Si una operación tiene mayor prioridad, entonces debe realizarse primero.

Pongamos esto en práctica y resolvamos el ejemplo anterior otra vez: 2 + 2 × 2 = 2 + 4 = 6. La respuesta correcta es 6.

❗ Si la expresión tiene 2 o más operaciones iguales, entonces se resuelven en orden de izquierda a derecha. La multiplicación y división son operaciones equivalentes y el orden en que se resuelven depende únicamente del orden en el que aparecen en la expresión. Lo mismo aplica para la suma y resta.

Arriba se puede ver el ejemplo para la solución de la expresión 12 ÷ 3 × 6 — 12 ÷ 6 × 3. De acuerdo con las reglas, primero se deben resolver la división y multiplicación, moviéndose de izquierda a derecha, después nuevamente la división y multiplicación ubicadas en el lado derecho de la expresión y solo al final resolver la restar. Si el orden se modifica, la respuesta será incorrecta.

Regla 3. Elevar un número a una potencia o sacarle raíz debe hacerse antes de proceder con otras operaciones

✅ Si la expresión tiene un número que se tiene que elevar a alguna potencia o realizar su operación inversa (sacar raíz), entonces es necesario hacer esto antes de resolver las operaciones aritméticas básicas.

Por ejemplo, intentemos resolver a qué es igual 4 + 2 + 2² + 3². Para esto, primero se debe elevar a la potencia el número 2 y 3. Como resultado se obtiene 4 + 2 + 4 + 9. Después, al sumar todos estos números se obtiene 19.

❌ Aquí es muy fácil cometer el error de sumar los números con el mismo exponente (es decir, 2² y 3²) y después elevar el resultado a la potencia.

Regla 4. Las operaciones entre paréntesis siempre se resuelven en primer lugar

✅ Si una parte de la expresión está entre paréntesis, se debe resolver en primer lugar. Después debes elevar a la potencia o sacar raíz y al final resolver el resto de las operaciones tomando en cuenta la prioridad y moviéndote de izquierda a derecha.

En la imagen superior tenemos un simple ejemplo. A la izquierda está la solución en donde se toma en cuenta el orden correcto en la jerarquía de operaciones: primero se obtiene el resultado entre paréntesis, después se hace la multiplicación una a la vez y al final se hace la suma. Del lado derecho no se cumple la jerarquía de operaciones, todas ellas se resuelven de izquierda a derecha y, por consiguiente, el resultado es incorrecto.

✅ Las reglas de prioridad y orden de izquierda a derecha aplican también para las operaciones entre paréntesis.

En las expresiones largas se pueden colocar números encima de las operaciones que correspondan al orden en qué se deben de resolver, tal como se muestra en el ejemplo anterior. Esto hará que el proceso sea más fácil.

Cómo recordar la jerarquía de operaciones

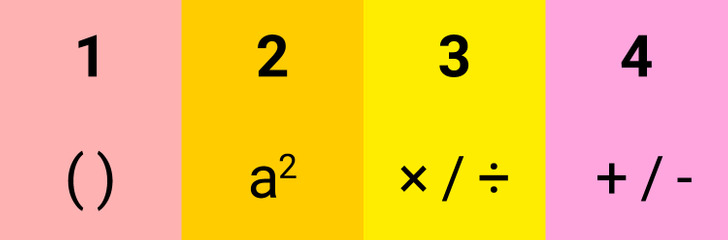
1. Si en la expresión hay paréntesis, primero se resuelve todo lo que hay en su interior.

2. Si en la expresión se debe elevar un número al cuadrado o sacar una raíz, resuelve esto antes de pasar a las demás operaciones.

3 y 4. Entre las 4 operaciones aritméticas básicas, la multiplicación y división tienen mayor prioridad que la suma y la resta, por lo cual deben realizarse primero. Las operaciones que tienen la misma prioridad se resuelven por orden, de izquierda a derecha.

Respuestas de los ejemplos del inicio del artículo

• 8 ÷ 4 × 2 = 2 × 2 = 4

Este es un ejemplo muy sencillo. Es poco probable que te hayas equivocado al resolverlo, ya que intuitivamente resolviste las operaciones una por una moviéndote de izquierda a derecha.

• 6 ÷ 2(1 + 3) = ?

Este ejemplo parece sencillo, pero es capaz de causar confusión incluso en los catedráticos de matemáticas. Eso está relacionado con el hecho de que se pueden obtener diferentes respuestas dependiendo de cómo se resuelva. Por ejemplo, una solución puede ser la siguiente: 6 ÷ 2(1 + 3) = 6 ÷ 2(4) = 3 * 4 = 12. Pero si recurrimos a la propiedad distributiva en donde a(b+c) es igual a a × b + a × c, entonces se obtiene que 6 ÷ 2(1 + 3) = 6 ÷ ((2 × 1) + (2 × 3)) = 6 ÷ (2 + 6) = 6 ÷ 8 = ³/₄. Esto ocurre debido a que la expresión se puede interpretar de diferente forma. Como resultado, las respuestas también serán distintas. En algún sentido, esto es muy parecido a la situación cuando debido a una formulación incorrecta y orden de palabras en la oración se tienen diferentes sentidos.

• 3(4 + 1) + 6² ÷ 3 — 7 = 3 × 5 + 6² ÷ 3 — 7 = 3 × 5 + 36 ÷ 3 — 7 = 15 + 36 ÷ 3 — 7 = 15 + 12 — 7 = 20

En esta expresión es fácil cometer diferentes errores, pero la forma correcta de resolverla es la siguiente: primero se resuelven las operaciones entre paréntesis, después el número 6 se eleva al cuadrado, posteriormente se tiene que resolver la multiplicación, luego la división y por último la suma y resta. Se obtiene un resultado análogo si recordamos la propiedad distributiva (en donde a(b+c) es igual a a × b + a × c) y se resuelve el ejemplo de la siguiente manera: 3(4 + 1) + 6² ÷ 3 — 7 =

((3 × 4) + (3 × 1)) + 6² ÷ 3 — 7 = (12 + 3) + 6² ÷ 3 — 7 = 15 + 36 ÷ 3 — 7 = 15 + 12 — 7 = 20.