Para qué sirven las fórmulas de productos notables
La multiplicación de números no nos parece tan difícil hasta que nos enfrentamos a ejemplos complejos en donde no solo hay números, sino también variables. Para transformar o simplificar tales expresiones, puedes utilizar fórmulas de productos notables. Pero solo a primera vista pueden parecer complicadas.
En Ideas en 5 minutos te explicaremos qué son las fórmulas de productos notables, cómo entenderlas y usarlas a la hora de resolver varios problemas.
Para qué se necesitan las fórmulas de productos notables
A menudo nos enfrentamos a este tema en las clases de álgebra. A primera vista, todo parece complicado, pero las fórmulas de productos notables realmente ayudan a realizar cálculos de forma rápida y compacta en determinadas situaciones.

Situación 1. Supongamos que en tu mente no quieres elevar grandes números a una determinada potencia y luego realizar operaciones matemáticas con los resultados obtenidos. Mira la imagen de arriba: en lugar de elevar al cuadrado los números 89 y 88 y luego restar los números grandes, como se muestra en la imagen de la izquierda, es más fácil usar la fórmula de la diferencia de cuadrados
a2 − b2 = (a − b) × (a + b), como se muestra en la imagen de la derecha.
De igual modo, para elevar un número grande al cuadrado, puedes usar la fórmula del cuadrado de una diferencia (a − b)2 = a2 − 2ab + b2. Por ejemplo: 792 = (80 − 1)2 = 6400 − 160 + 1 = 6241.
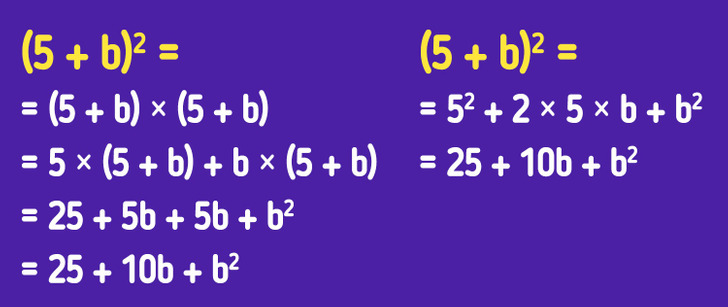
Situación 2. Supongamos que quieres deshacerte del paréntesis en una expresión realizando pocos pasos. Para eliminar los de la expresión (5 + b)2, como la de la imagen de arriba del lado derecho, usamos la fórmula del binomio al cuadrado (a + b)2 = a2 + 2ab + b2. Como resultado, obtenemos la expresión 25 + 10b + b2. Se puede obtener el mismo resultado sin usar esta fórmula, pero realizando todos los pasos consecuentemente. Sin embargo, con la fórmula es más rápido y sencillo.
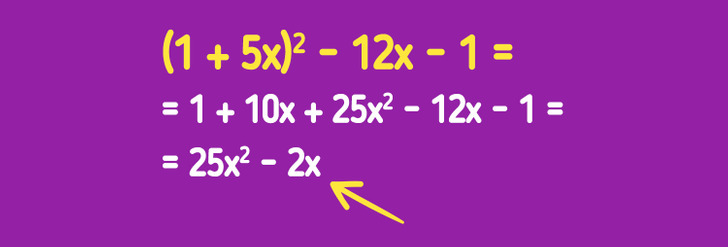
Situación 3. Supongamos que tienes que llevar un polinomio (suma de productos y variables) a su forma estándar. Para hacerlo, en la imagen de arriba volvemos a usar la fórmula del binomio al cuadrado (a + b)2 = a2 + 2ab + b2 y convertimos (1 + 5x)2 − 12x − 1 en 25×2 − 2x.
Qué fórmulas de productos notables existen

No es tan difícil aplicar estas fórmulas. Basta con realizar los pasos sistemáticamente.
Ejemplo 1. Tomemos la parte derecha de la diferencia de cuadrados (a − b) × (a + b) y eliminemos los paréntesis, obteniendo (a − b) × (a + b) = a2 + ab − ab − b2. Dado que ab − ab = 0, al final obtenemos (a — b) × (a + b) = a2 — b2.
Ejemplo 2. Tomemos la parte derecha de la fórmula de suma de cuadrados (a + b)2 y eliminemos la potencia, obteniendo (a + b)2 = (a + b) × (a + b). Eliminemos los paréntesis, obteniendo a2 + ab + b2 + ab, y luego a2 + 2ab + b2. Como resultado, obtenemos (a + b)2 = a2 + 2ab + b2.
Ejemplo 3. A menudo se puede encontrar la fórmula del trinomio cuadrado perfecto. Pero ¿qué hacemos si necesitamos la fórmula de su diferencia? Intentemos obtenerla por nuestra propia cuenta: (a − b − c)2 = (a − b − c) × (a − b − c) = a2 − ab − ac − ba + b2 + bc − ca + cb + c2 = a2 − 2ab − 2ac + b2 + 2bc + c2. Se puede escribir de la siguiente manera: (a − b − c)2 = a2 + b2 + c2 − 2ab − 2ac + 2bc.

Puedes aplicar las fórmulas del cubo de un binomio de la misma manera.
Ejemplo 1. Tomemos la parte derecha de la fórmula (a − b) × (a2 + ab + b2) y eliminemos los paréntesis, obteniendo a3 + a2b + ab2 − ba2 − ab2 − b3 = a3 + a2b − ba2 − b3 = a3 − b3. Como resultado, obtenemos (a − b) × (a2 + ab + b2) = a3 − b3.
Cómo recordar las fórmulas de los productos notables
Por lo general, las fórmulas de los productos notables se aprenden de memoria en las escuelas. Si se te olvidan por casualidad, entonces puedes usar algunos pasos para simplificar la expresión, como hicimos en los ejemplos anteriores. Pero existen métodos que pueden facilitar ese proceso.

Por lo general, cuando se trata de la enésima potencia de una suma o diferencia (suma de cuadrados, diferencia de cuadrados, suma de cubos, diferencia de cubos, entre otras), lo más difícil es recordar los coeficientes y signos de la fórmula. Pero si dibujas un triángulo de Pascal, no tendrás que aprenderlos de memoria.
Para empezar, escribe tres veces el número uno: uno en el medio y los otros dos a los lados, pero de modo que todos formen un triángulo.
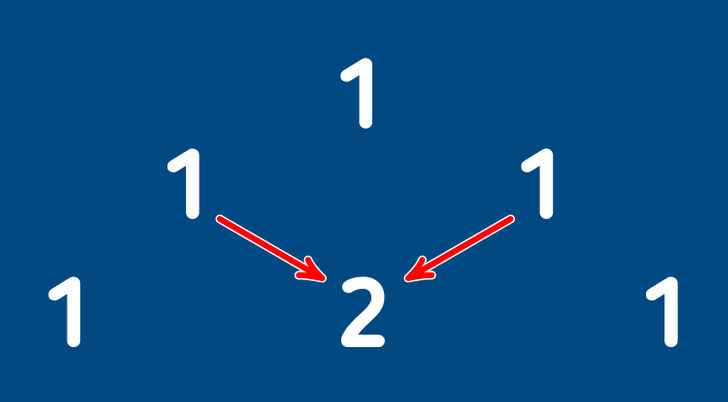
La línea con un solo 1 se considerará nula. Por lo tanto, tenemos dos 1 en la primera línea. Para obtener la segunda línea, colocaremos nuevamente los 1 por los lados y entre ellos colocaremos el número cuyo resultado se obtiene al sumar los dos números de arriba. De este modo, en el medio de la segunda línea aparecerá un 2.
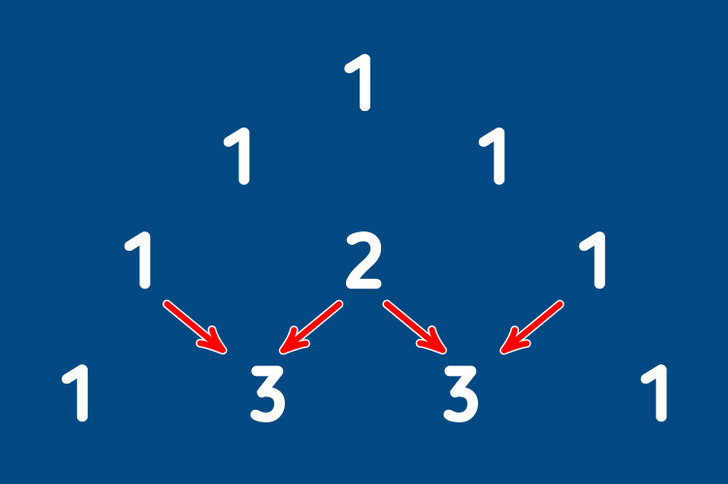
Ahora escribimos la tercera línea. Por los lados ponemos dos números de 1 y luego entre ellos volvemos a sumar aquellas cifras que se obtienen al sumar los números superiores, es decir, 2 números tres.
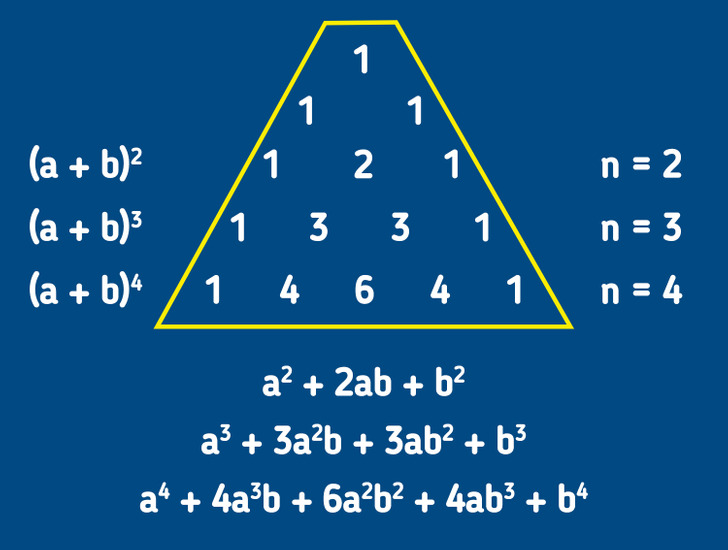
De esta forma continuaremos completando el triángulo hasta la cuarta línea. ¿Qué obtenemos? Mira la imagen de arriba. En cada fila tenemos los coeficientes de la descomposición de un binomio en un polinomio.
Nos falta ver los signos. ¿Cómo se deben recordar? El primero de ellos será el mismo que aparece en el binomio. Si tenemos una suma, el signo será + en toda la expresión. Si es una diferencia, entonces el primer signo será un — y posteriormente los signos se alternarán.
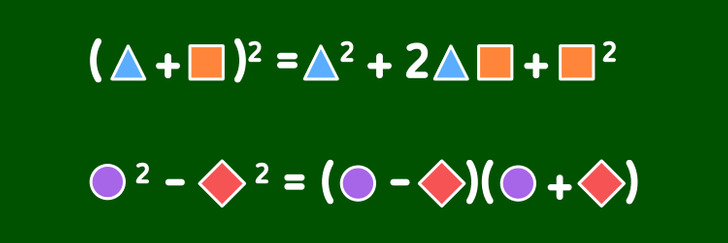
Método alternativo. A algunas personas les resulta más fácil recordar fórmulas imaginando figuras abstractas en lugar de variables, como se muestra en la imagen de arriba.
Cómo leer correctamente las fórmulas de productos notables
- a2 + b2 = (a + b)2 − 2ab
La suma de cuadrados de dos términos es igual a la suma de estos términos al cuadrado menos dos veces el producto de los términos.
- a2 − b2 = (a − b) × (a + b)
La diferencia de cuadrados de dos términos es igual al producto de su diferencia y su suma.
- (a + b)2 = a2 + 2ab + b2
El cuadrado de una suma es igual al cuadrado del primer término, más el doble producto del primero por el segundo, más el cuadrado del segundo.
- (a − b)2 = a2 − 2ab + b2
El cuadrado de una resta es igual al cuadrado del primer término, menos el doble producto del primero por el segundo, más el cuadrado del segundo.
- a3 + b3 = (a + b) × (a2 − ab + b2)
La suma de cubos de dos expresiones es igual al producto de suma de estos términos por el cuadrado imperfecto de su diferencia.
- a3 − b3 = (a − b) × (a2 + ab + b2)
La diferencia de cubos de dos expresiones es igual al producto de suma de estos términos por el cuadrado perfecto de su diferencia.
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
Una suma al cubo es igual al cubo del primero, más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo.
- (a − b)3 = a3 − 3a2b + 3ab2 − b3
Una resta al cubo es igual al cubo del primero, menos el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, menos el cubo del segundo.
Cuáles son los errores más frecuentes al aplicar estas fórmulas

- Confunden la suma de cuadrados y el cuadrado de la suma, la diferencia de cuadrados y el cuadrado de la diferencia, la suma de cubos y el cubo de la suma, la diferencia de cubos y el cubo de la diferencia.
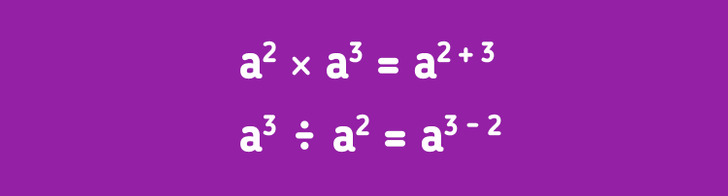
- Confunden las fórmulas de producto notable y las fórmulas de multiplicación abreviadas y división de variables con potencias.
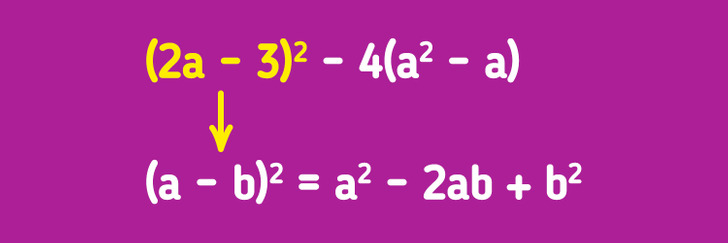
- No notan que una expresión puede tener una parte que se simplificará o resolverá usando la fórmula de producto notable.
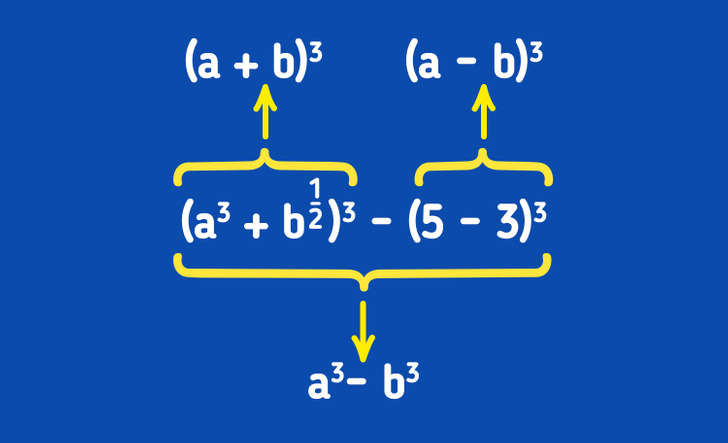
- No ven la fórmula para el producto notable en una expresión, porque se les olvida que a veces puede haber expresiones completas en lugar de una variable.