Qué tipos de figuras geométricas existen
Muchos puntos dan una línea y con varias líneas unidas entre sí pueden obtenerse figuras geométricas en un plano y en el espacio. Por lo tanto, un conjunto arbitrario de puntos nos permite crear estas figuras. Puede ser un cuadrado, un cubo, un círculo o una esfera, así como formas más complejas y ambiguas, tales como un icosaedro, que puede representarse de dos maneras distintas.
Ideas en 5 minutos te propone averiguar cómo se diferencian los tipos de figuras geométricas.
Figuras geométricas planas
Una figura geométrica plana se ubica en un espacio bidimensional, donde los objetos se caracterizan solo por su largo y ancho. Por lo tanto, se distinguen las siguientes:
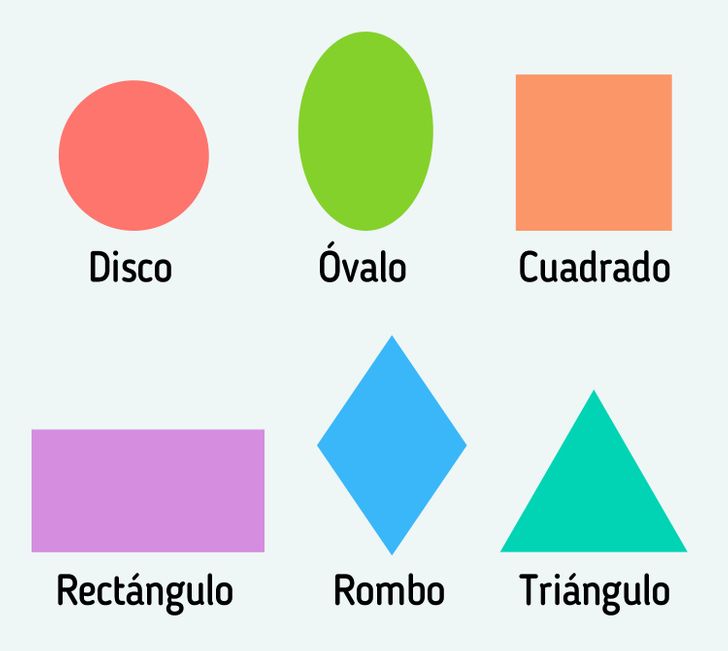
- El disco es una figura que no tiene esquinas y en la que todos los puntos se ubican a la misma distancia del centro.
- El óvalo tiene una forma que se parece a la del huevo. Tampoco tiene esquinas.
- El cuadrado es una figura con 4 lados iguales y 4 ángulos rectos.
- El rectángulo es una figura similar a un cuadrado. Tiene 4 lados, los cuales se cruzan en ángulos rectos. A diferencia de un cuadrado, solo los lados opuestos del rectángulo son iguales. Si usas un segmento de línea para conectar cualquier esquina con la opuesta, entonces puedes obtener una diagonal. Tanto el cuadrado como el rectángulo tienen diagonales iguales.
- El rombo es una figura con 4 lados iguales, pero estos no se cruzan en ángulos rectos. Las esquinas opuestas del rombo son iguales. Al igual que el cuadrado y el rectángulo, es un cuadrilátero.
- El triángulo es una figura con 3 esquinas y 3 lados. Los puntos en los que se cruzan estos lados se llaman vértices.
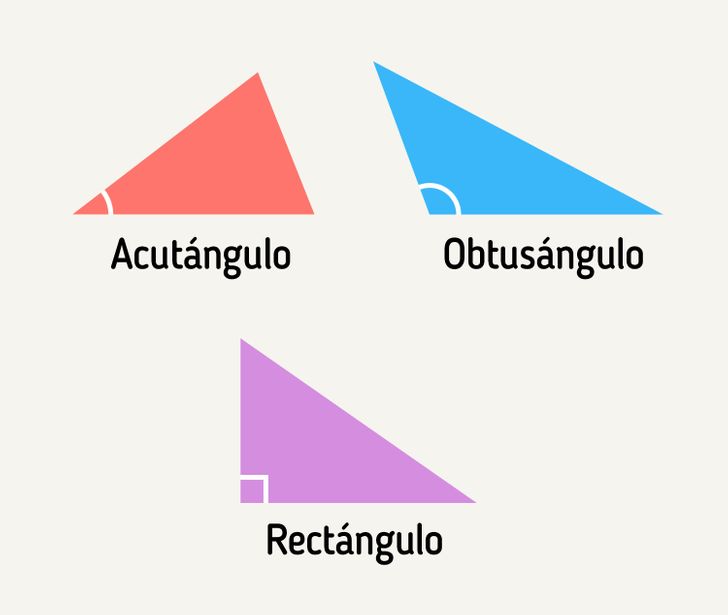
Tipos de triángulos según el tamaño de sus ángulos:
🔷 Acutángulo: todos los ángulos son agudos (cada uno tiene menos de 90°)
🔷Obtusángulo: un ángulo es obtuso (tiene más de 90°)
🔷Rectángulo: un ángulo es recto (tiene 90°)
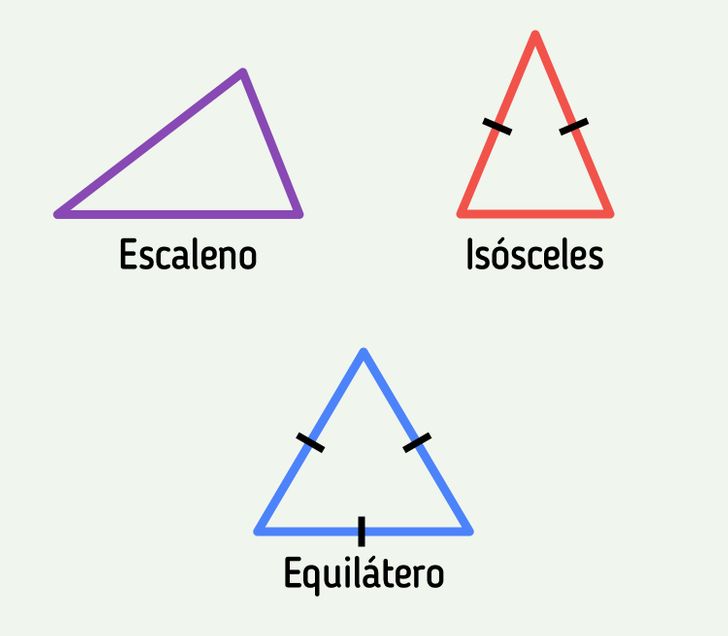
También existen tipos de triángulos según la longitud de sus lados:
🔶 El equilátero tiene 3 lados iguales
🔶 El isósceles tiene 2 lados iguales
🔶 El escaleno tiene 3 lados diferentes

Hemos hablado sobre las principales figuras geométricas en un plano. Pero existen otras. Por ejemplo:
- El trapezoide es un cuadrilátero con al menos 2 lados paralelos. Por lo tanto, un cuadrado, un rombo y un rectángulo pueden considerarse casos especiales de trapecio.
- El paralelogramo es un cuadrilátero en el que los lados opuestos son paralelos en pares. De este modo, un rectángulo, un cuadrado y un rombo se consideran casos especiales de un paralelogramo.
- El pentágono es un polígono regular con 5 lados. Tiene todos sus lados y ángulos iguales.
- El hexágono es un polígono regular con 6 lados iguales, y sus esquinas forman 6 triángulos equiláteros.
- La cruz es una figura que consta de 2 líneas o rectángulos que se cruzan.
- La estrella es un polígono plano no convexo. Puede tener tres, cuatro, cinco puntas (como en la imagen superior) y más.

Una figura geométrica puede ser convexa si todos los puntos del segmento que conecta cualesquiera dos puntos de la figura pertenecen también a ella. El disco, la esfera, el óvalo y el triángulo son formas convexas. Los cuadriláteros pueden ser tanto convexos como no convexos. Por ejemplo, en la imagen superior podemos ver la misma figura: deltoides. Es un cuadrilátero, cuyos lados pueden agruparse en dos pares de lados adyacentes iguales. Del lado izquierdo se encuentra un deltoide convexo, y del lado derecho uno no convexo.
Cuerpos geométricos
Los cuerpos geométricos se definen por estar ubicados en un espacio tridimensional en donde los objetos se caracterizan por su largo, ancho y alto, y también tienen profundidad o grosor. Pueden destacarse los siguientes cuerpos geométricos:
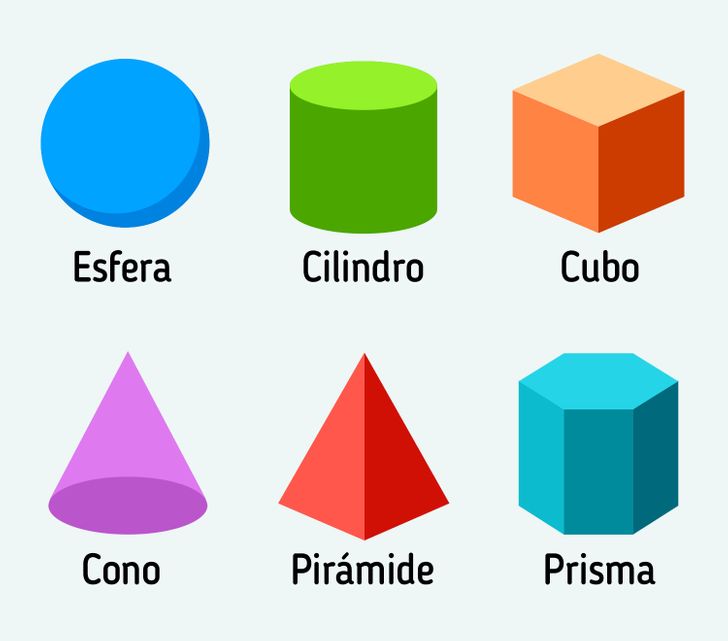
- La esfera puede definirse análoga a un disco en el espacio. Todos los puntos ubicados en la superficie de la esfera están a la misma distancia de su centro.
- El cono está formado por un conjunto de rayos que conectan todos los puntos de una determinada curva plana con un solo punto en el espacio (el vértice del cono). Los conos se diferencian entre sí. Por ejemplo, si su base es un disco, entonces puede ser un cono circular recto.
- El cilindro tiene forma de rodillo. Su base consiste en círculos, y entre ellos se encuentra una parte de una superficie cilíndrica.
- El cubo es un cuerpo poliédrico: todas sus caras son cuadradas. Además, tiene 6 caras, 12 aristas y 8 vértices. Un cubo también puede llamarse hexaedro regular o hexágono.
- La pirámide es un poliedro con un polígono en su base y sus caras están representadas por triángulos que tienen un vértice común.
- El prisma es un poliedro que consta de dos caras iguales y paralelas llamadas bases, y de caras laterales que son paralelogramos. En la imagen superior se muestra un ejemplo particular de un prisma hexagonal. Tiene 8 caras, 18 aristas y 12 vértices.

Si un poliedro convexo consta de polígonos regulares idénticos y tiene simetría espacial, entonces se llama poliedro regular o sólido platónico. En un espacio tridimensional se distinguen cinco de estos poliedros regulares. El nombre de cada uno de ellos proviene del nombre griego del número de sus caras:
- El tetraedro o pirámide triangular. Las caras de este poliedro son 4 triángulos.
- El hexaedro o cubo.
- El octaedro es un poliedro cuyas caras son 8 triángulos equiláteros. Si cortas un octaedro a la mitad, puedes obtener dos pirámides iguales.
- El dodecaedro es un poliedro con 12 caras, y todas son pentágonos regulares.
- El icosaedro es un poliedro cuyas caras son 20 triángulos regulares.
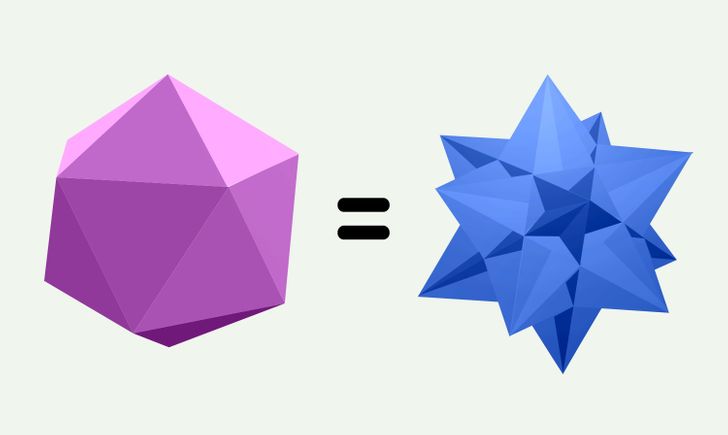
Además, un icosaedro regular puede ser tanto convexo como no convexo. Pero el término “icosaedro regular” se refiere más a menudo a una forma convexa, y una no convexa se llama gran icosaedro.