4 Métodos para explicar fracciones a un niño
Es bastante difícil para los escolares dominar el tema de las fracciones y de las operaciones que se realizan con ellas. Pero si el niño se familiariza con los conceptos básicos a través del juego y de aquello que le resulta conocido, es posible evitar dificultades en el aprendizaje.
Ideas en 5 minutos te trae una guía sencilla que permitirá que incluso un niño en edad preescolar comprenda qué son las fracciones.
Qué es una fracción
Tenemos una pizza deliciosa y dos personas hambrientas. Dividamos una pizza entera en dos porciones iguales para que cada persona tenga la mitad. La mitad, o 1/2, de una pizza es una fracción. Las dos mitades forman una unidad entera.
Se pueden extraer dos conclusiones del ejemplo anterior:
- La fracción es parte de un todo
- La fracción es menor que la unidad entera
Digamos que teníamos una pizza y la dividimos en cuatro partes. Una de esas piezas ya se ha comido. Como resultado, nos quedamos con tres piezas de cuatro. Esta cantidad se puede escribir como 3/4. En el papel, la línea divisoria se puede escribir horizontal o diagonalmente.
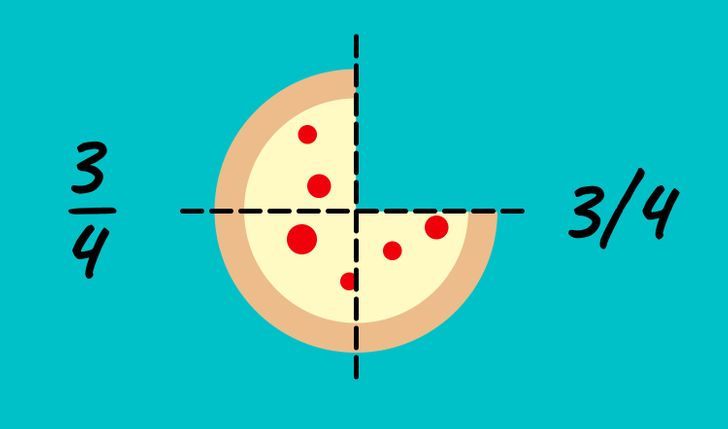
- El número de abajo (o el de la derecha) es el denominador: nos dice en cuántas partes se ha dividido el número entero.
- El número de arriba (o de la izquierda) es el numerador: nos dice con cuántas de estas partes estamos tratando.
Cuando dividimos un número entero en partes, cuantas más de estas partes haya, menores serán, y viceversa. Por ejemplo, tenemos dos pizzas: una la dividimos equitativamente entre dos personas y la otra entre cuatro. En el primer caso, cada persona recibió la mitad de la pizza (1/2), y en el segundo, solo una cuarta parte (1/4).
Gracias a estos simples ejemplos y a las herramientas que tengamos a mano, podemos explicarles a los niños cómo dividir una unidad en partes y qué acciones simples se pueden realizar con las fracciones.
Método número 1: utilizamos un constructor infantil

Las piezas de Lego son útiles para mostrar las diferentes partes de una unidad. El número de protuberancias de cada ladrillo ayuda a transmitir mejor la esencia del concepto de las partes de un todo.
- Si tomamos una pieza con ocho protuberancias como una unidad, entonces una pieza cuadrada con cuatro protuberancias será la mitad, con seis serán 3/4 y una pieza con una sola protuberancia será 1/8.
- Cuando una pieza larga con cuatro protuberancias actúa como una unidad, 1/2 será una pieza con dos protuberancias y 1/4 será una pieza con una protuberancia.
- Si tenemos una pieza larga con tres protuberancias como una unidad, entonces 2/3 simbolizará una pieza con dos protuberancias y 1/3, una pieza con una protuberancia.
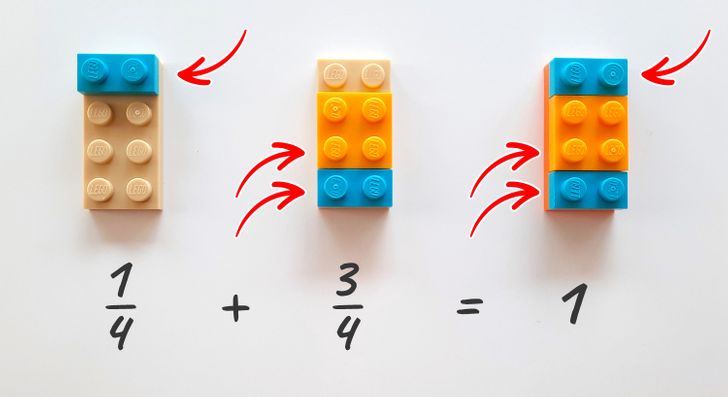
Puedes seguir explicando de manera similar acciones simples con fracciones que tienen el mismo, o común, denominador. En la imagen de arriba, se muestra cómo sumamos 1/4 y 3/4, obteniendo como resultado una unidad. En este caso, el uso de piezas de diferentes colores ayuda a ver qué lugar ocupará en una unidad cada una de sus partes como resultado de la suma.
Tarea: Usando piezas de Lego como en el ejemplo anterior, prueba sumar y restar fracciones con un denominador común junto a tu hijo.
Método número 2: dividimos los círculos en partes
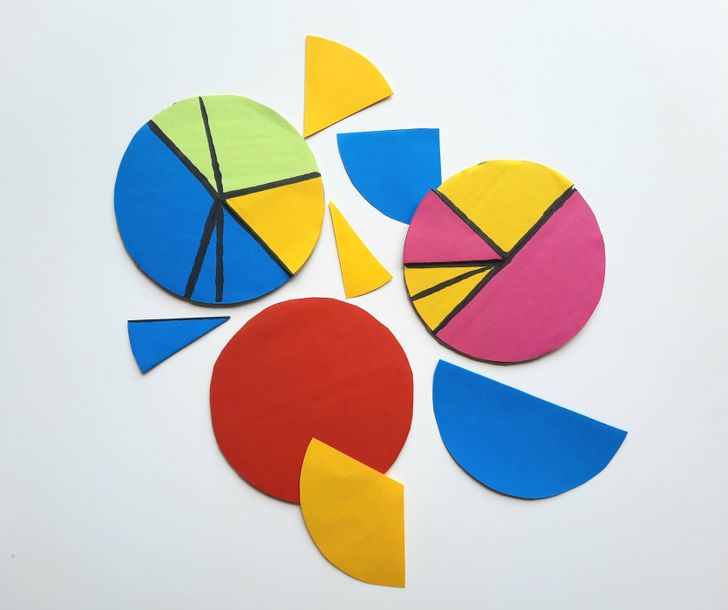
Una fracción se puede representar como una parte de un entero. Comprender cómo son estas o aquellas fracciones ayudará al niño no solo a compartir una pizza u otras delicias redondas con amigos, sino también a distinguir la hora en un reloj: de esta manera será más fácil explicar qué es un cuarto de hora y cuánto tiempo pasará cuando la manecilla del reloj pase la mitad del círculo.
Para explicar la división en fracciones, corta tres círculos idénticos de cartón.
- Cubre el primer círculo completamente con papel de un color. Simbolizará la unidad.

- Divide el segundo círculo en dos mitades trazando una línea con un lápiz común. Cubre una mitad con papel de un color. Pega sobre la otra mitad papel de un color contrastante y luego vuelve a dividirla por la mitad para obtener dos cuartos. Divide uno de los cuartos por la mitad nuevamente, obteniendo dos octavos. Pega sobre uno de estos octavos papel de color. El resultado es un círculo dividido por la mitad, un cuarto y dos octavos.
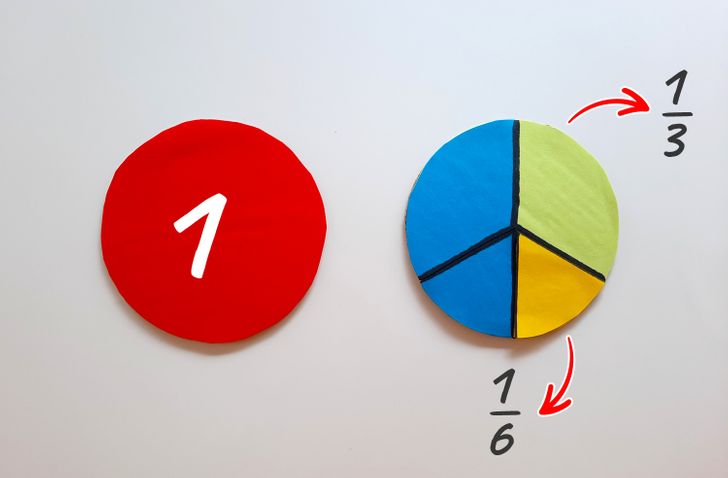
- Ahora divide el tercer círculo en tres partes iguales. Pega sobre un tercio papel de un color. Divide el otro tercio por la mitad para obtener dos partes iguales a 1/6 del círculo. Pega sobre uno de ellos papel de un color contrastante. Te queda la mitad del círculo, sobre el que también hay que pegar papel de un color. De esta manera, puedes demostrar cuánto de un todo es 1/3 y 1/6, y que cuando se suman forman 1/2 de un círculo entero.

Además, puedes recortar fracciones individuales de papel de color para superponerlas sobre la unidad (el primer círculo) y así mostrar claramente su valor, así como realizar operaciones simples de suma y resta dentro del círculo.
Tarea: Prueba armar junto con tu hijo un círculo completo usando diferentes combinaciones de sus partes.
Método número 3: completamos una escala en partes

Un número entero se puede representar como una escala, donde las fracciones son divisiones de la escala. Con un marcador y una regla, dibuja una escala de 12 divisiones en una hoja grande de papel. Puede ser parecida a la de la imagen de arriba. Cada división mide 2 cm de largo. Ahora toma plastilina y enróllala en bolitas del tamaño de una cereza.

Invita a tu hijo a tomar una bolita y a ubicarla de modo que ocupe una división. Para llenar toda la escala, necesitamos 12 de estas bolitas, pero solo tenemos una. Por lo tanto, tenemos 1/12 del total.

Ahora agreguemos otra bola a la escala. Se puede poner junto a la primera e incluso pegarlas para hacer un par. Si tomamos seis de esos pares, llenamos toda la escala. Pero solo tenemos uno de seis, o 1/6 del total. De esto se puede sacar una conclusión más:
- 1/6 = 1/12 +1/12

Ahora agreguemos otra bola. Para llenar toda la escala, solo necesitamos cuatro de estos tripletes de bolas. Hasta ahora tenemos solo una cuarta parte, o 1/4, del total requerido para llenar la escala. De esta imagen se deduce que:
- 1/4 = 1/12 +1/12 +1/12
- 1/4 = 1/6 +1/12
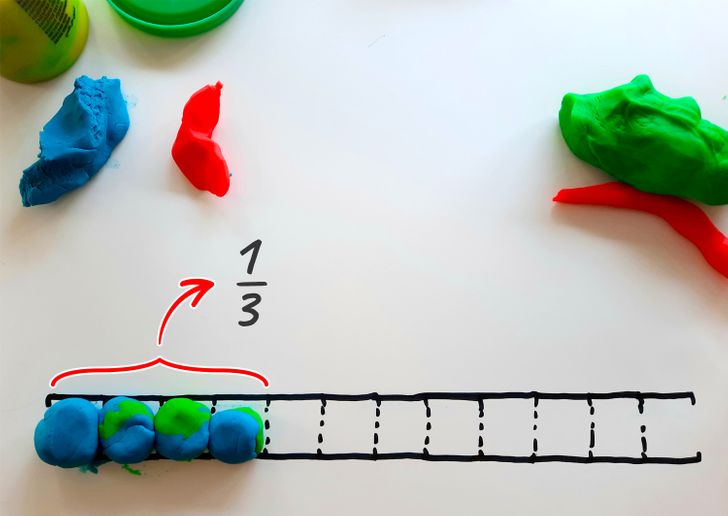
Agreguemos otra bola para llenar cuatro divisiones a la vez. Para llenar toda la escala, necesitamos tres de estos grupos. Solo tenemos uno de los tres disponible, o 1/3. Si recuerdas que una división significa 1/12, y dos divisiones son 1/6, entonces resulta que:
- 1/3 = 1/12 +1/12 +1/12 +1/12
- 1/3 = 1/6 + 1/6
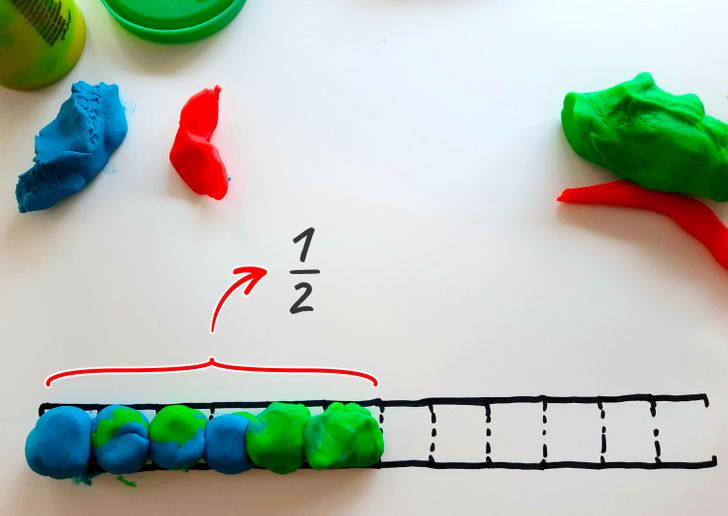
Ahora agreguemos dos bolas a la escala para tener seis de ellas. Así completamos la mitad de las divisiones, o 1/2. De esto podemos deducir que:
- 1/2 = 1/12 +1/12 +1/12 +1/12 +1/12 +1/12
- 1/2 = 1/6 + 1/6 + 1/6
- 1/2 = 1/3 +1/6
- 1/2 = 1/4 +1/4
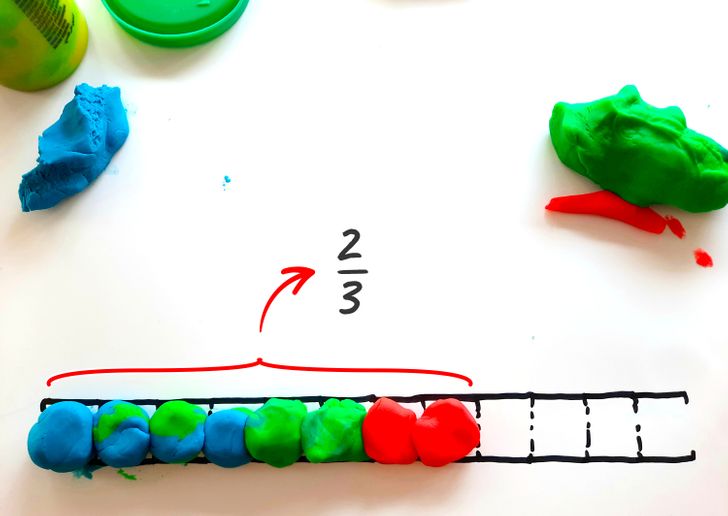
Agrega un par de bolas más para tener ocho. Así completamos 2/3 de toda la escala. ¿De qué se componen dos tercios?
- 2/3 = 1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12
- 2/3 = 1/6 + 1/6 + 1/6 + 1/6
- 2/3 = 1/3 +1/3
- 2/3 = 1/4 + 1/4 + 1/6
- 2/3 = 1/2 + 1/6

Completemos una división más con una bola. Esto cerrará nueve celdas. Esto es tres cuartas partes de la escala total. ¿Cómo se puede representar este número?
- 3/4 = 1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12
- 3/4 = 1/6 + 1/6 + 1/6 + 1/6 +1/12
- 3/4 = 1/3 +1/3 +1/12
- 3/4 = 1/2 + 1/6 +1/12

Finalmente, si sumamos tres bolas más, llenaremos toda la escala, obteniendo un número entero.
Método número 4: denotamos la proporción

Dibuja a siete personas. Que sean diferentes en el color de la ropa y el cabello, la postura y la presencia de ciertos objetos. En este caso, consideramos a un grupo de personas como una unidad.

Dos de cada siete (2/7) tienen un globo en la mano y cinco de cada siete (5/7) no. En este caso, la fracción no solo divide el todo, sino que ayuda a indicar la proporción.
Por tanto, todo se puede dividir. Como ejemplo alternativo, considera una taza de chocolate caliente:
☕ = 🍫🍫 / 🥛🥛🥛,
que es 2/5 de chocolate delicioso y 3/5 de leche fresca.
Qué son los decimales

Toma una hoja de papel y dibuja una tabla cuadrada de 100 celdas sobre ella. La tomaremos como una unidad dividida en 100 partes-celdas idénticas.
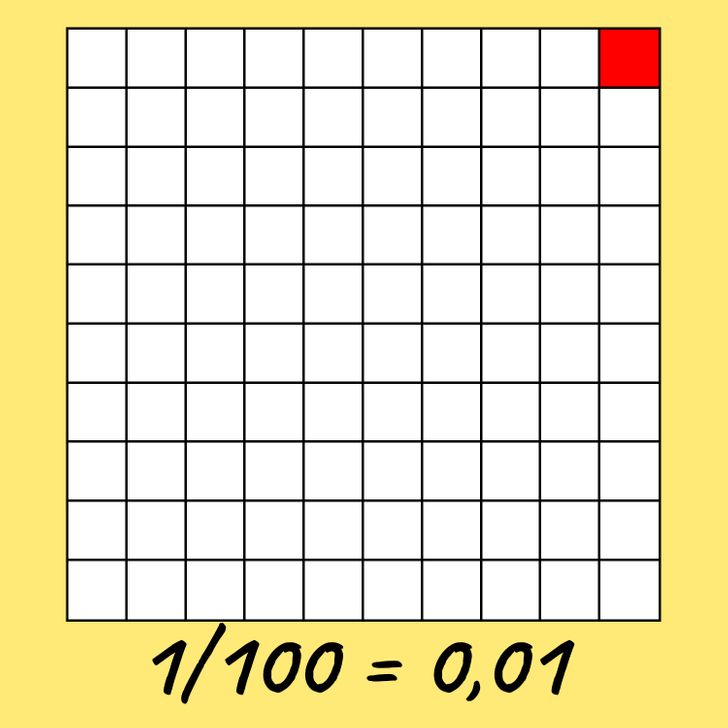
Ahora pintaremos una celda. Esta es una de las 100 partes de la tabla. Tal número en forma de una fracción común se ve como 1/100. Pero se puede anotar en una línea separada por comas para separar la parte entera de la parte fraccionaria:
1/100 = 0,01
Todo lo que está a la izquierda de la coma es un número entero. Todo lo que está a la derecha es parte de un número entero: décimas, centésimas, milésimas, diezmilésimas y menores, pero siempre múltiplos de diez. En otras palabras, si el denominador de una fracción simple es 10, 100, 1000, 10 000 y similares, entonces estamos hablando de una fracción decimal. Esta notación simplifica la forma de una fracción, por ejemplo:
- 0,8 es 8/10,
- 14,89 es 1489/100,
- 3,14159 es 314 159/100 000.
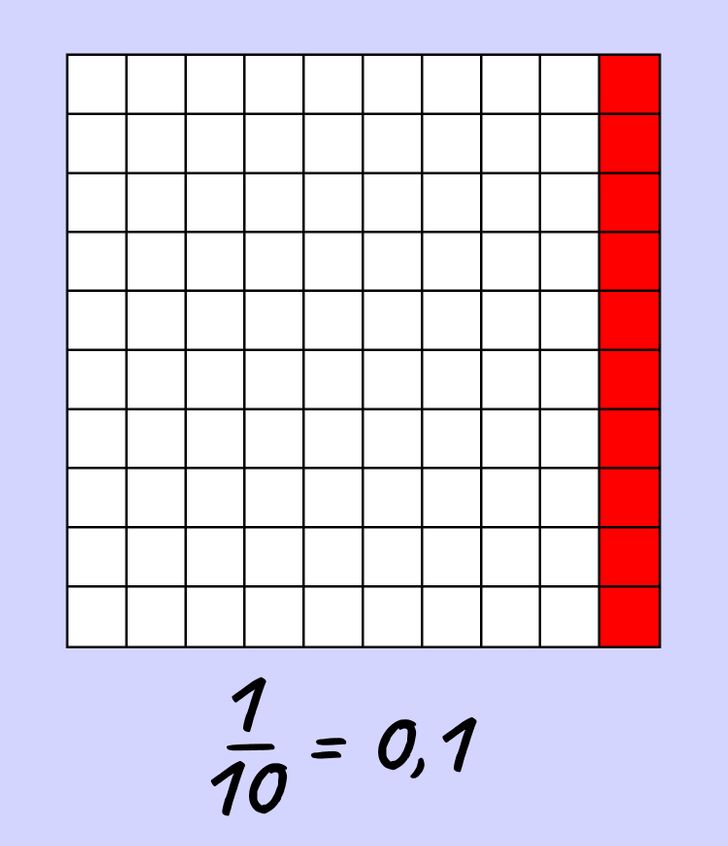
Ahora completemos toda la columna de la tabla. La tabla completa consta de 10 columnas de este tipo, por lo que podemos decir que una columna es igual a una décima parte de la tabla.
En lugar de 1/10, anotaremos el número como 0,1.
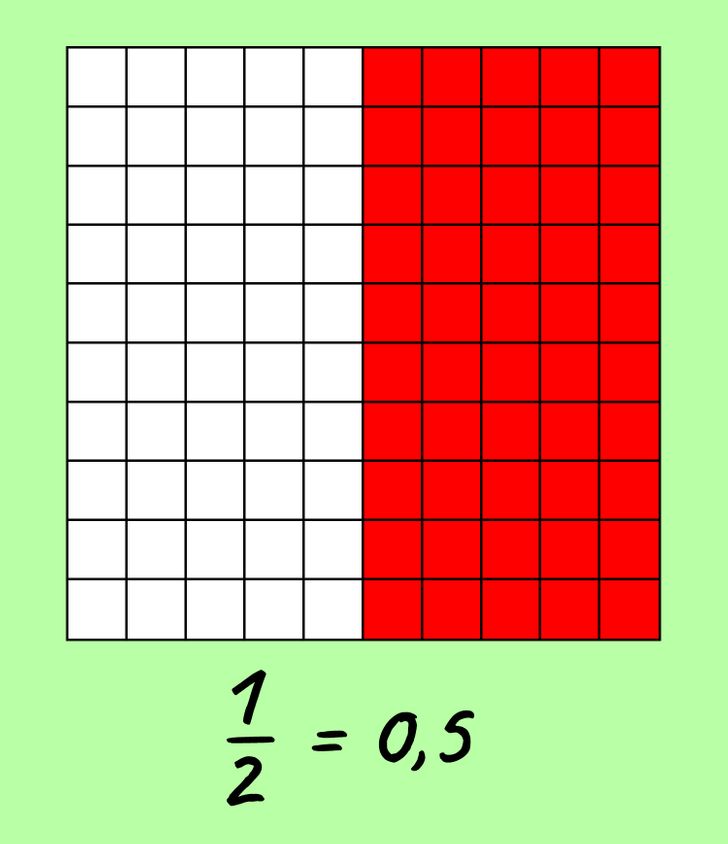
Si completamos cuatro columnas más, entonces podemos decir que hemos pintado cinco décimas, o 0,5. La imagen de arriba muestra que esto es exactamente la mitad o 1/2 de la tabla.
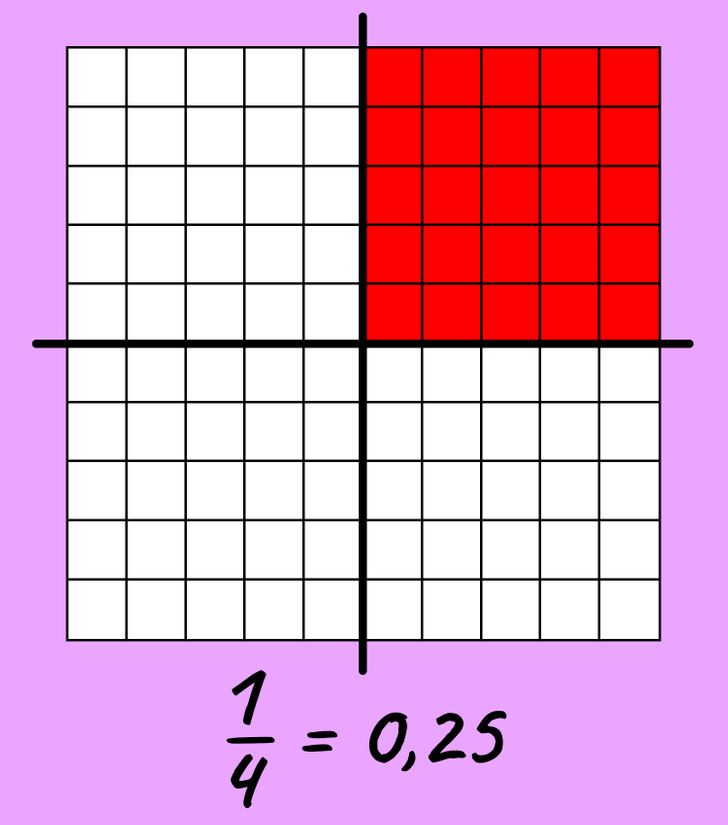
Digamos que nuevamente tomamos una tabla vacía y la dividimos con líneas en cuatro partes iguales. Pintamos una de las cuatro partes: resultan ser 25 celdas de 100, o 0,25. Por tanto, vemos que 1/4 = 0,25.
Es decir que los mismos números se pueden anotar en forma de fracciones comunes y decimales:
- 3/4 = 0,75
- 1/2 = 0,5
- 1/4 = 0,25
- 1/5 = 0,2
- 1/10 = 0,1
- 1/100 = 0,01
Tarea: Dibuja varias tablas cuadradas vacías de 100 celdas y pídele al niño que coloree las celdas que representen diferentes fracciones y fracciones decimales, comparándolas entre sí. Esto lo ayudará a ver y a recordar visualmente que, por ejemplo, 3/4 es más de 0,3 o 0,4.