Por qué no se puede dividir entre cero
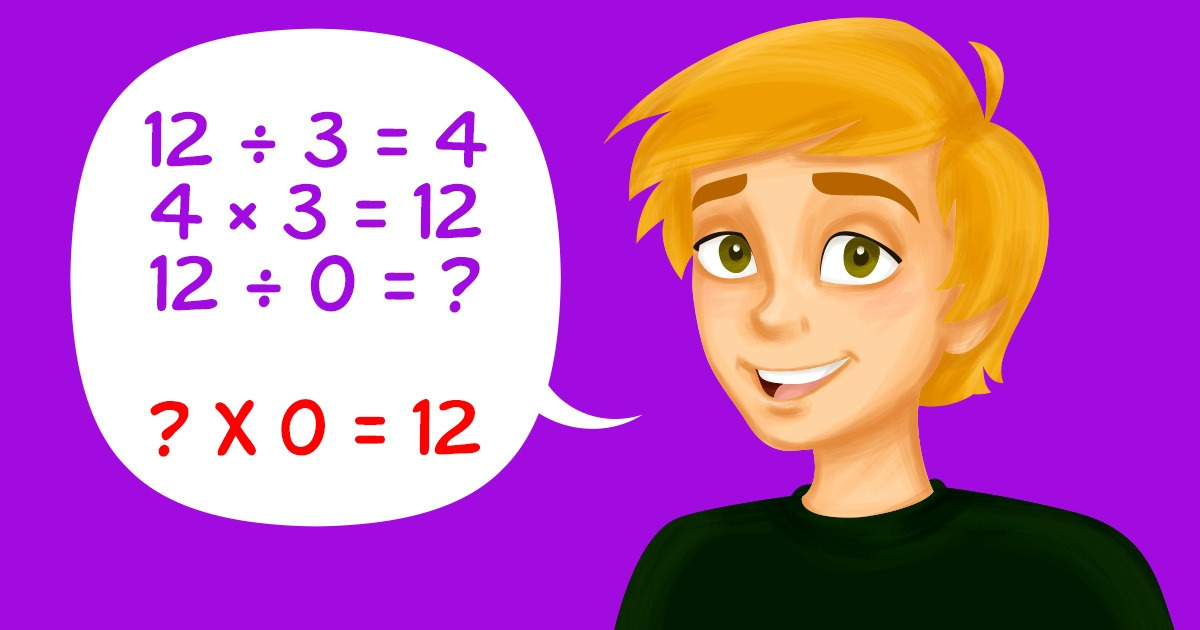
En la escuela nos enseñaron que no se puede dividir entre 0. Incluso hay chistes sobre la aparición de agujeros negros porque alguien intentó hacerlo. Pero ¿cuál es la verdadera razón de esto?
En Ideas en 5 minutos decidimos abordar este tema en detalle y descubrir por fin qué ocurre si se rompe este preciado tabú.
Qué es la división
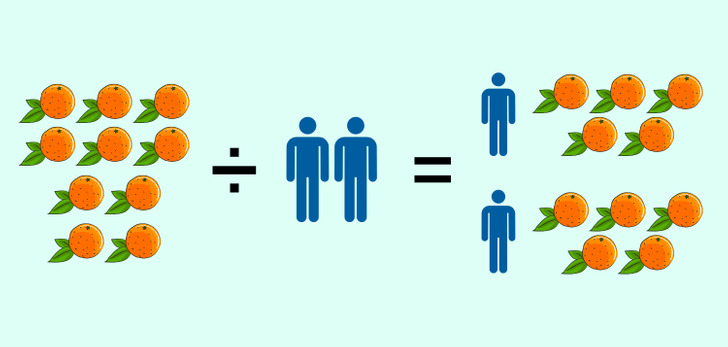
En un nivel aritmético simple, la división consiste en dividir un grupo de objetos en partes iguales. Por ejemplo, tomamos 10 naranjas para repartirlas entre 5 personas sentadas en una mesa. Cada una recibirá una cantidad de fruta igual a 10 ÷ 5, es decir, 2. Si en la mesa hubiera una persona, recibiría 10 ÷ 1, es decir, 10 naranjas.
Entonces surge la siguiente pregunta: ¿cuántas de las 10 naranjas le tocarán a cada uno si hay 0 personas sentadas en la mesa?
Por qué no se puede dividir entre 0
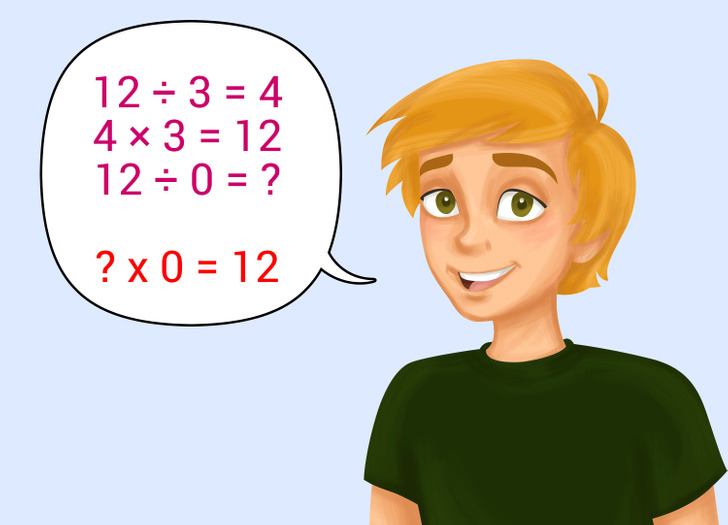
La cuestión es que dividir entre 0 no tiene sentido, porque cualquier intento de hacerlo lleva a más y más contradicciones. He aquí un ejemplo.
Por regla general, después de dividir, podemos retroceder utilizando la multiplicación. Para la ecuación r = a ÷ b, debe ser cierto a = r × b.
Si asumimos que b = 0, entonces obtenemos que r × 0 = a.
Si 12 ÷ 3 = 4, entonces 4 × 3 = 12.
Si 12 ÷ 0 = ?, entonces, al parecer, deberíamos obtener ? × 0 = 12.
Pero dado que cualquier número multiplicado por 0 es igual a 0, debemos obtener r × 0 = 0.
Resulta que para cualquier valor de r, si a ≠ 0, la ecuación no se puede resolver.
Qué pasa con el infinito
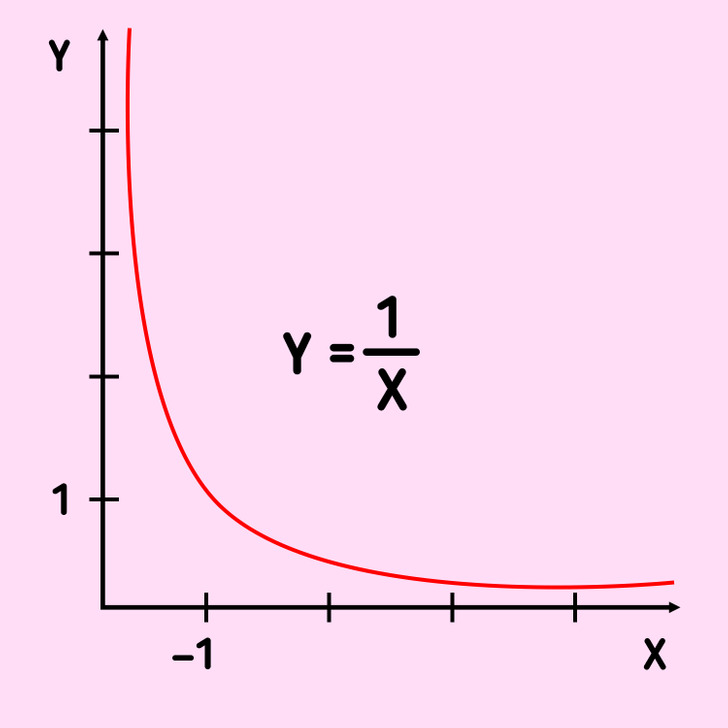
Se puede suponer que una fracción cuyo denominador es 0 es igual a infinito. Esta idea no carece de lógica. Probablemente, te hayas dado cuenta de que cuando dividimos un número entre otro cada vez más pequeño, obtenemos una cifra cada vez más grande. Para ilustrarlo, tenemos un ejemplo:
20 ÷ 5 = 4
20 ÷ 2 = 10
20 ÷ 0,5 = 40
20 ÷ 0,0000005 = 40 000 000
Se puede observar que el divisor disminuye infinitamente y el cociente aumenta también infinitamente, tendiendo así a infinito. Sin embargo, tender a infinito y ser igual a infinito son dos conceptos completamente diferentes. Porque el infinito no es un número concreto, sino una idea abstracta. Si intentamos tratar el infinito como un número (por ejemplo, en la ecuación 1 : 0 = ∞), nos toparíamos con las siguientes anomalías matemáticas:
1 ÷ 0 = ∞ = 2 ÷ 0
1 = 0 × ∞ = 2
En consecuencia,
1 = 2
En este escenario, llegaríamos a la declaración de que todos los números enteros son iguales entre sí, y todo el sistema colapsaría.
Qué pasa si dividimos 0 entre 0
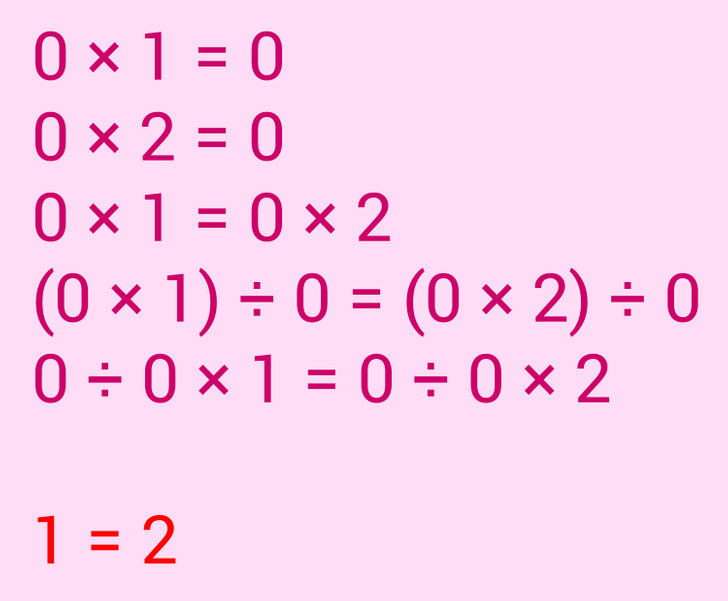
Veamos otro ejemplo.
Supongamos que
0 × 1 = 0
0 × 2 = 0
Entonces es cierto lo siguiente:
0 × 1 = 0 × 2
Al dividir ambos lados entre 0 obtenemos:
(0 × 1) ÷ 0 = (0 × 2) ÷ 0
0 ÷ 0 × 1 = 0 ÷ 0 × 2
Es decir,
1 = 2
El error aquí es suponer que para dividir 0 entre 0 se aplican las mismas reglas que para dividir entre otros números.
Resumiendo todo lo anterior, la regla “no se puede dividir entre 0” queda más clara: no se puede dividir por 0 no porque vaya a ocurrir algo crítico, sino porque simplemente eso no tiene sentido.