Qué es la teoría de la probabilidad en términos sencillos

Imagina que un artista callejero te invita a jugar a un juego: él tira los dados y tú solo tienes que adivinar el número total de los dos dados para ganar un premio. No hay forma de predecir el número entre el 2 y el 12 que obtendrás al tirar los dados. Pero si eliges un siete, tendrás más posibilidades de ganar que si eliges un dos. Esto es lo que nos enseña la teoría de la probabilidad.

En Ideas en 5 minutos, intentaremos explicar de forma sencilla en qué consiste la teoría de la probabilidad.

Qué estudia la teoría de la probabilidad

Simplifiquemos la situación con los dados tomando una moneda corriente. Si la lanzas, saldrá una de dos: cara o cruz. Intenta lanzar una moneda 100 veces y verás que cada lado sale aproximadamente el mismo número de veces. Así que hay un 50 % de posibilidades de que salga cara o cruz.

Si lanzas un par de dados, obtendrás un total de 2 a 12 (según el número de puntos de las caras de los dados). El número total de puntos de los dados será un valor aleatorio. En otras palabras, un valor aleatorio es una expresión numérica del resultado de un evento aleatorio.

Lanzar una moneda hacia arriba te dará cara o cruz. Se trata de dos acontecimientos aleatorios. Cada uno de ellos puede o no ocurrir. Un suceso es un concepto que está en el centro de la teoría de la probabilidad.

La teoría de la probabilidad es una rama separada de las matemáticas que estudia los patrones asociados a los fenómenos aleatorios: los sucesos aleatorios, las variables aleatorias, sus propiedades y las operaciones con ellas.

Qué es el espacio de los sucesos elementales

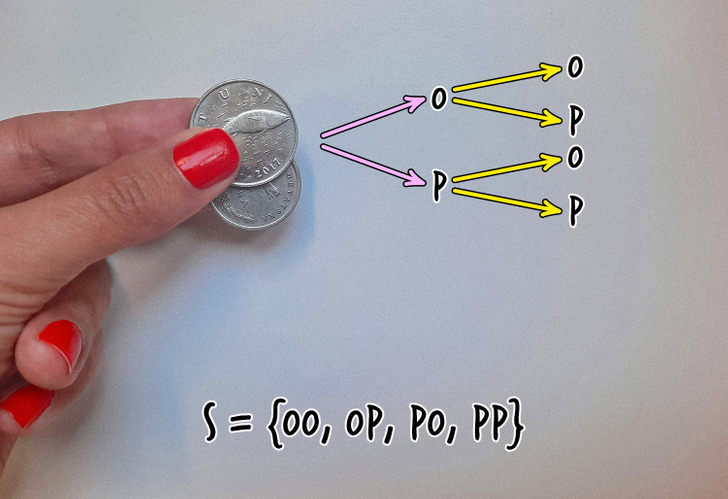
Tomemos dos monedas. Si se lanza cada una, saldrá cara o cruz, uno de los dos posibles sucesos. ¿Cuántos sucesos posibles puedes obtener si lanzas dos monedas al mismo tiempo?

Fíjate en la imagen de arriba: aquí hemos marcado con P el suceso en el que sale cruz, y con O el suceso en el que sale cara. Supongamos que en el primer lanzamiento de una moneda sale cara y en el otro sale cruz. Luego, en el segundo lanzamiento, cada moneda puede volver a salir con cara o cruz, lo que daría 4 combinaciones posibles según los resultados de los dos lanzamientos. Lo que hemos dibujado arriba se llama árbol de probabilidad. Representa todos los posibles sucesos independientes en este ensayo.

Entonces, las combinaciones de OO, OP, PO y PP representan el conjunto de todos los diferentes resultados de nuestro ensayo, llamado espacio de sucesos elementales, y se denotan con la letra S.

Cómo calcular la probabilidad utilizando la fórmula clásica

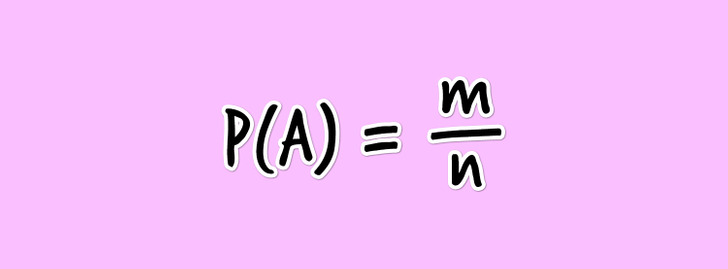
La probabilidad de que un suceso se produzca o no en un determinado ensayo se puede calcular mediante la fórmula:

P (A) = m/n

P denota la probabilidad del suceso, A es el propio suceso en cuestión, n es el número total de todos los diferentes resultados elementales de ese ensayo y m es el número de resultados elementales por los que puede ocurrir el suceso A.

Por ejemplo, tomemos un paquete de caramelos de colores. Hay 51 caramelos en la bolsa, 6 de ellos son azules. La probabilidad de encontrar un caramelo azul en este paquete (suceso A en este caso) es: P (A) = m/n. Significa 6/51, o un poco más del 11 % (podemos escribir la probabilidad en forma de porcentaje en lugar de fracción).

• Si todos los caramelos del paquete fueran azules, la probabilidad de que te toque un caramelo azul sería: 51/51 = 1.
• Si quieres calcular cuál es la probabilidad de que te salga un caramelo morado de este paquete, obtendrás: 0/51 = 0.

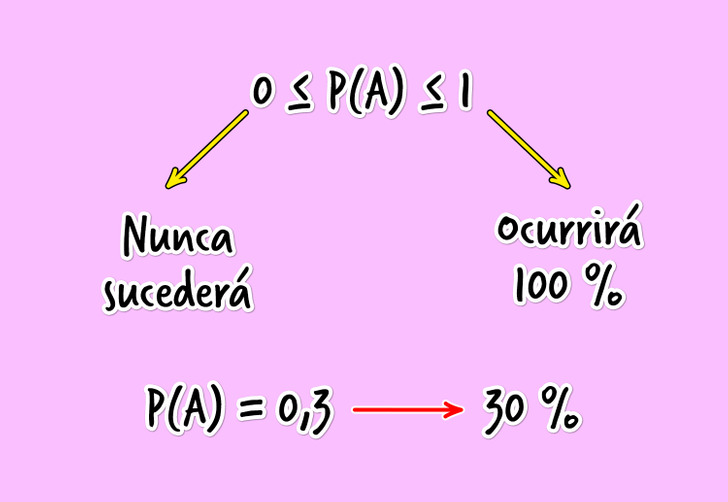
Así, empíricamente, llegamos a la conclusión de que la probabilidad tiene varias propiedades:

• Si la probabilidad de un suceso es 1, ocurrirá 100 %.
• Si la probabilidad de un suceso es 0, nunca ocurrirá.
• Entre el cero y el uno habrá un número positivo que describa la probabilidad de un evento aleatorio concreto. Si la probabilidad de un suceso es de 0,3, significa que con un 30 % de probabilidad ocurrirá.

De esto podemos concluir que para la probabilidad de cualquier evento es cierto 0 ≤ P (A) ≤ 1.

Cómo resolver problemas sencillos de teoría de la probabilidad

Problema n.º 1. Hay 15 manzanas diferentes en una cesta: 10 manzanas verdes y 5 manzanas rojas. ¿Cuál es la probabilidad de sacar una manzana amarilla de la cesta?

Solución. Utilicemos la fórmula P (A) = m/n. En este caso n = 15 y m = 0. En consecuencia, la probabilidad de obtener la manzana amarilla de la cesta es: P (A) = 0/15 = 0. En otras palabras, es imposible.

Problema n.º 2. Hay 36 cartas en la baraja. Una carta ha sido sacada de allí. ¿Cuál es la probabilidad de que sea una carta de picas?

Solución. Utilicemos la fórmula P (A) = m/n. En este caso n = 36 y m = 9 (que es el número de cartas de las picas que hay en toda la baraja). Entonces la probabilidad del suceso buscado es: P (A) = 9/36 = 0,25 %, es decir, el 25 % de que saques una carta de picas.

Teoremas de suma y multiplicación en probabilidades

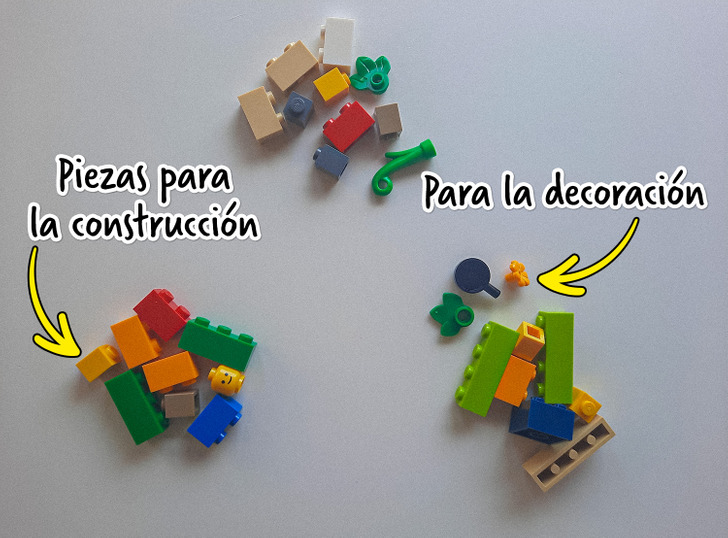
Imagina que hay tres pilas de 10 piezas de construcción en cada pila frente a ti. La primera pila tiene 8 piezas para construir una casa, la segunda pila tiene 7 y la tercera pila tiene 9, todas las demás piezas son para decorar y armar personas. Tomas una pieza al azar de cada pila. ¿Cuál es la probabilidad de que las tres partes sean adecuadas para construir la casa?

Para aclarar: si tomas una pieza de construcción de una pila, no significa que vayas a tomar o no una pieza similar de las otras dos pilas. En otras palabras, estos sucesos son independientes entre sí (la probabilidad de que se produzca uno de ellos es independiente de los demás sucesos del conjunto que estamos considerando).

Entonces, estamos considerando tres eventos independientes. Calculemos la probabilidad de extraer una pieza de construcción para cada pila:

• 1.ª pila: 8/10, o sea 0,8, o sea 80 %
• 2.ª pila: 7/10, o 0,7, o 70 %
• 3.ª pila: 9/10, o 0,9, o 90 %

Para calcular la probabilidad de que estos tres sucesos independientes ocurran juntos, tenemos que multiplicarlos: 0,8 × 0,7 × 0,9 = 0,504. Resulta que la probabilidad de que las tres piezas resulten ser de construcción es de 0,504, es decir, más del 50 %.

Resolvimos este problema utilizando el teorema de la multiplicación de la probabilidad, que se ve así:

P (A × B) = P (A) × P (B|A)

La fórmula significa que la probabilidad del producto de dos sucesos es igual al producto de la probabilidad de uno de ellos y la probabilidad condicional del otro, calculada bajo la condición de que el primero haya ocurrido (la parte de la fórmula escrita como P (B|A) denota la probabilidad del suceso B bajo la condición de que el suceso A haya ocurrido). Donde:

• El suceso A se llama independiente del suceso B si la probabilidad del suceso A es independiente de que el suceso B haya ocurrido o no.
• El suceso A se llama dependiente del suceso B si la probabilidad del suceso A cambia en función de que ocurra o no el suceso B.

Si se trata de eventos independientes, la fórmula es la siguiente:

P (A × B) = P (A) × P (В)

Problema. En un cuenco hay bolas: 2 naranjas y 3 azules. Se sacan dos bolas seguidas del cuenco. ¿Cuál es la probabilidad de que ambas bolas sean de color naranja?

Solución. Denotemos la extracción de dos bolas naranjas en una fila como evento A. Será el producto de dos sucesos: A = A1 × A2, donde:

A1 es la aparición de la bola naranja en el primer intento de extracción del cuenco,

A2 es la aparición de la bola naranja en el segundo intento de sacarla del cuenco.

P (A1) = 2/5

P (A2) = (2-1) / (5-1) = 1/4

P (A) = P (A1 × A2) = 2/5 × 1/4 = 0,1. Resulta que la probabilidad de que ambas bolas resulten ser de color naranja es solo de 0,1, es decir, del 10 %.

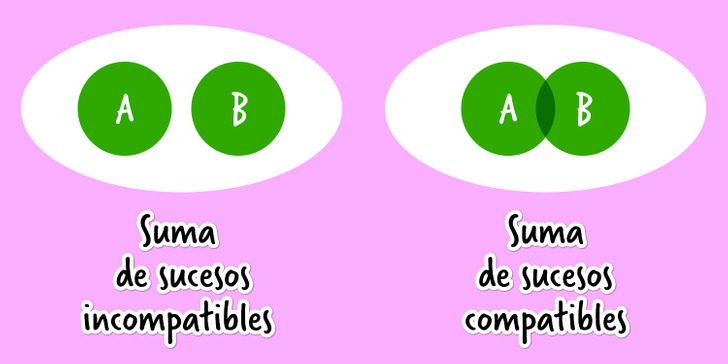
La suma de dos sucesos A y B es un suceso A + B, en el cual el suceso A o el B, o ambos sucesos, ocurren simultáneamente. Si los sucesos son incompatibles (es decir, la ocurrencia de un suceso excluye la ocurrencia del otro dentro del mismo ensayo), entonces puede ocurrir o el suceso A, o el suceso B.

Al lanzar una moneda obtendremos dos eventos opuestos y mutuamente excluyentes: saldrá cara o cruz. Cuando dos acontecimientos son opuestos, se indican con las mismas letras, pero se añade una raya o un apóstrofe sobre una de ellas. Por ejemplo, sería A y Ā o A y A’.

Imagina que tienes nueve peras en una bolsa de frutas: 4 verdes, 3 rojas y 2 amarillas. Escoges una de ellas al azar. ¿Cuál es la probabilidad de que no sea amarilla?

Para responder a la pregunta, encuentra la probabilidad de que te toque la pera verde (A) y la pera roja (B), y luego súmalas (A + B) para encontrar la probabilidad de que te toque una u otra (pero no la amarilla).

P (A) = 4/9

P (B) = 3/9 = 1/3

Estos dos hechos son incompatibles. Sumemos sus probabilidades entre sí:

P (A+B) = P (A) + P (B) = 4/9 + 1/3 = 7/9.

Resulta que la probabilidad de que la pera tomada no sea amarilla es de 7/9, es decir, más del 77 %.

Para resolver este problema, utilizamos la fórmula P (A + B) = P (A) + P (B) del teorema de la suma de probabilidades, que dice así: “La probabilidad de que ocurra uno de dos sucesos incompatibles es igual a la suma de las probabilidades de estos sucesos”.

Si se trata de sucesos compatibles (es decir, la ocurrencia de un suceso no excluye la ocurrencia de otro dentro del mismo ensayo), entonces la probabilidad de su suma se calcula mediante la fórmula P (A + B) = P (A) + P (B) − P (A × B).

Todas las fórmulas anteriores pueden utilizarse para resolver problemas sencillos de teoría de la probabilidad.

Bono: ¿Qué significa realmente la frase “probabilidad de lluvia” en el pronóstico del tiempo?

Imagina que el pronóstico del tiempo para mañana dice que hay un 30 % de probabilidades de lluvia. Esta cifra parece insignificante, y al día siguiente sales a pasear por la ciudad sin paraguas, para acabar empapado hasta los huesos. ¿Cómo es posible que esto ocurra cuando te han prometido que la probabilidad de lluvia es solo del 30 %?

No te apresures a regañar a los meteorólogos. Si la probabilidad de lluvia en el pronóstico del tiempo para tu ciudad es del 30 %, significa que hay un 100 % de posibilidades de que llueva, pero solo en el 30 % del territorio de la ciudad. Si ese día te moverás por la ciudad, incrementarás la posibilidad de mojarte.