Cómo explicarles a los niños qué son los porcentajes

Comprender los porcentajes puede ser difícil no solo para los niños, sino también para los adultos. Si necesitas obtener resultados rápidamente y no tienes un papel y un bolígrafo a mano, no te será útil lo que aprendiste en la escuela sobre este tema.

Ideas en 5 minutos te cuenta cómo explicarle a un niño los porcentajes de forma rápida y sencilla, y cómo resolverlos mentalmente con algunos trucos que los profesores de matemáticas no siempre revelan.

Qué es el porcentaje

Imagina que tenemos un enorme pastel cuadrado. Podrías tomarlo y dividirlo en 100 partes iguales. Hagámoslo de forma esquemática dibujando un gran cuadrado de 10 × 10 en una hoja de papel cuadriculada.

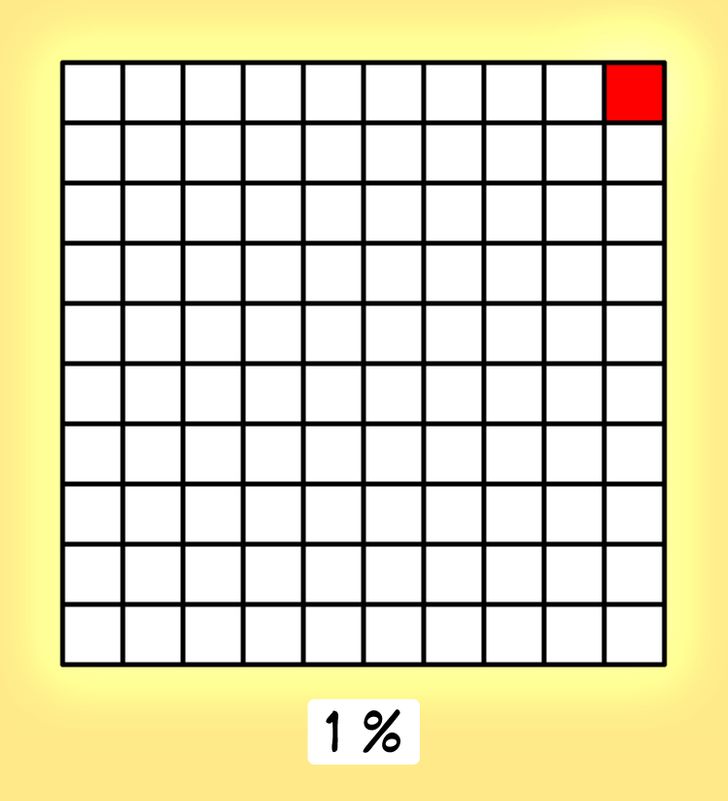
Vamos a colorear 1 cuadrado, que representa 1 rebanada. Será un porcentaje (1 %) de todo el pastel, ya que todo el pastel representa el 100 %.

De esta manera, cuando hablamos de porcentajes, pensamos en un número como un todo dividido en 100 partes iguales. La centésima parte del todo es el 1 % del número. En otras palabras, si dividimos cualquier número entre 100, obtenemos el 1 % de ese número.

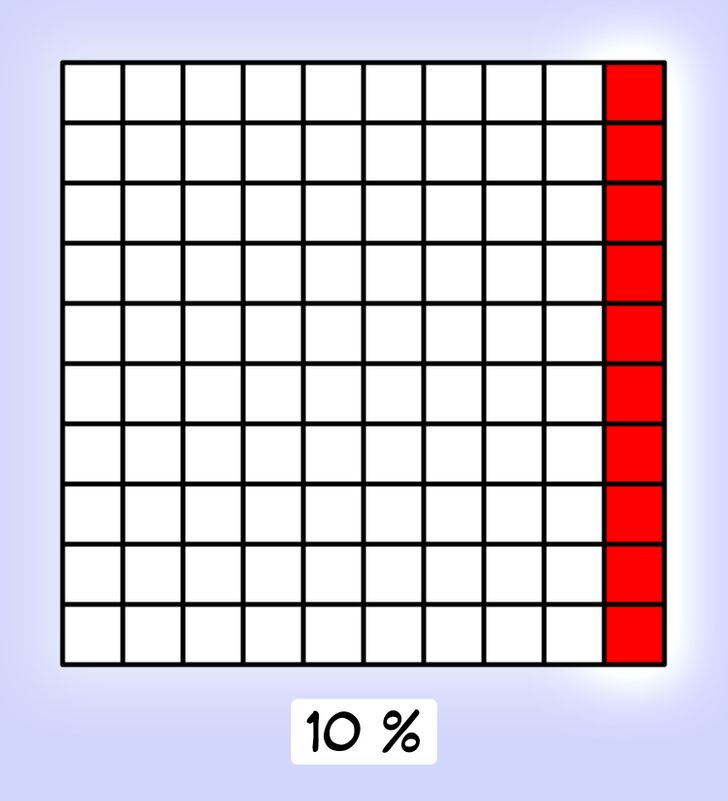
Utilizando un cuadrado de 100 casillas, es cómodo familiarizarse con el concepto de porcentajes y la parte de un todo que representan. Coloreemos 10 casillas: son 10 trozos de pastel, o el 10 % de todo el pastel.

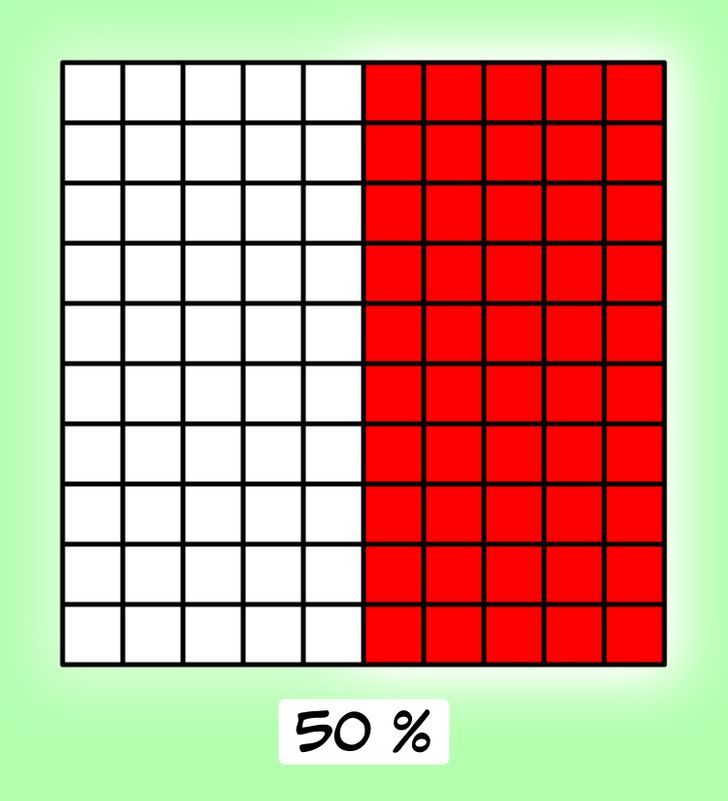
Ahora coloreamos la mitad de todo el cuadrado, es decir, 50 casillas. Se trata de 50 trozos de pastel, es decir, el 50 % del pastel entero. Cualquier porcentaje de un número entero se puede representar de la misma manera.

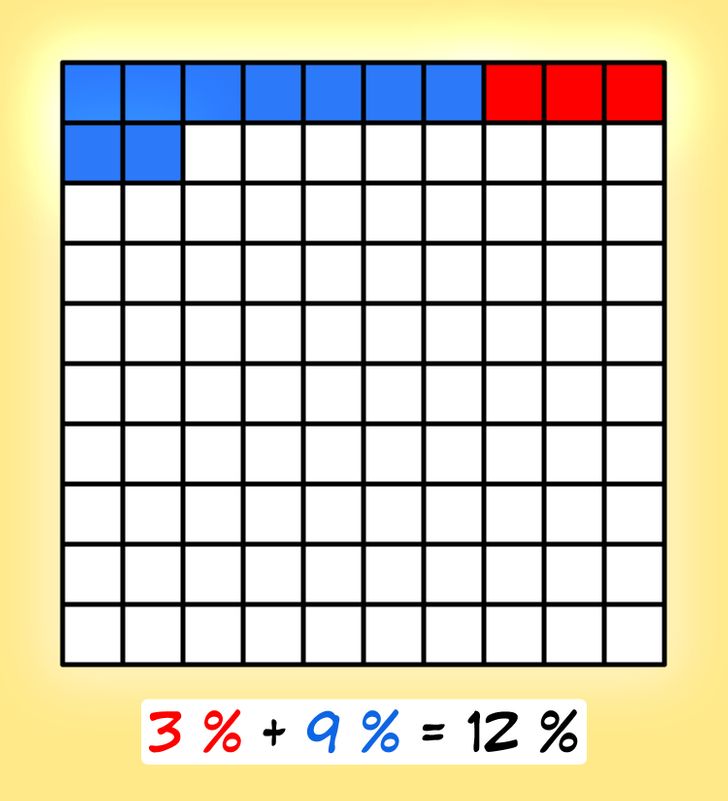
✅ Consejo: Utiliza este cuadrado de 10 × 10 para mostrar los números como porcentajes y compararlos entre sí. También puede utilizarse para realizar operaciones sencillas de suma y resta de porcentajes.

Ejemplo: En la imagen de arriba, hay 3 casillas rojas que corresponden al 3 % y 9 casillas azules que corresponden al 9 %. Contando todas las casillas coloreadas o sumando los números, obtenemos el 12 %.

Cómo calcular el porcentaje

La imagen de arriba muestra una tarea elemental. Es fácil de hacer: si un porcentaje es una manera de expresar una fracción cuyo denominador es 100, entonces el 17 % de 100 es 17, ya que expresado como fracción nos quedaría 17/100.

¿Pero qué pasa si quieres encontrar el porcentaje de un número diferente de 100? Por ejemplo, el 17 % de 400.

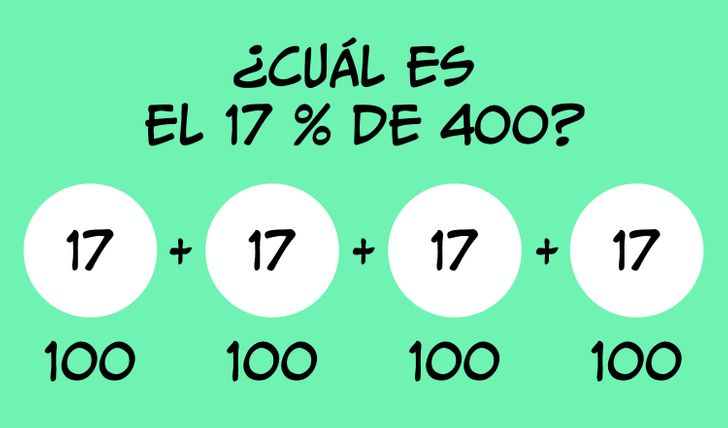
Podemos utilizar un truco e imaginar el número 400 como 4 centenas. Entonces consideramos que el 17 % del número 400 es el 17 % de cada cien que componen el 400. En ese caso basta con sumarlos y obtener la respuesta correcta:

17 + 17 + 17 + 17 = 68

Así sabemos que el 17 % de 400 es igual a 68. Pero este tipo de trucos no siempre alcanzan.

Ejemplo: Hay que obtener el 14 % de 550.

De la definición de porcentaje, recordamos que el 1 % es la centésima parte de un número entero (dividido en 100 partes iguales). Así, para encontrar el porcentaje de un número, divide el número entre 100 y multiplica el resultado por el número del porcentaje. Entonces tenemos que realizar dos pasos:

El resultado es que el 14 % del número 550 es 77.

En algunos problemas, la situación puede ser a la inversa, y hay que calcular a qué equivale el 100 %.

Ejemplo: ¿Cómo se obtiene el 100 % si el 65 % es 260?

Aquí actuaremos en la dirección contraria: primero averiguamos a qué equivale el 1 % y luego calculamos a qué equivale el 100 %. Entonces necesitamos:

El resultado es que el 100 % es igual a 400.

Esta es la forma de resolver los problemas de porcentaje, y es la forma más común de resolver los ejemplos de la escuela. Pero hay algunos trucos y métodos que harán el proceso de cálculo mucho más fácil.

Truco № 1: Intercambiar números y porcentajes

La regla para cualquier problema es: X % de Y = Y % de X. Luego puedes intercambiar números y porcentajes si eso facilita la solución del problema.

Digamos que hay que calcular el 4 % de 75:

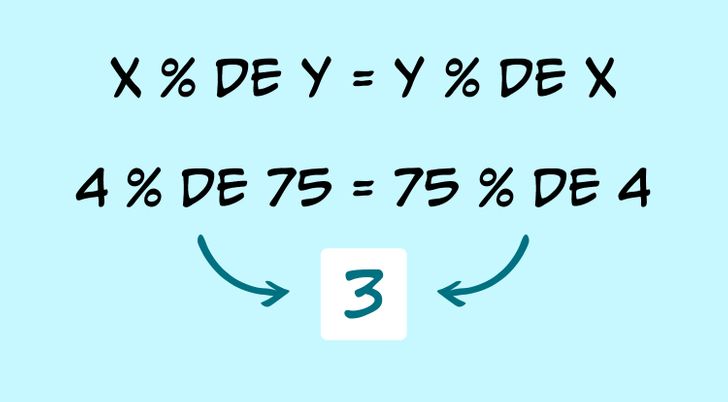
Cambiamos de lugar los números y los porcentajes y luego resolvemos el problema.

Si el 4 % de 75 = 75 % de 4,

entonces calculamos el 75 % de 4 y obtenemos el número 3.

Por lo tanto, el 4 % de 75 también es igual a 3.

Gracias a este truco, en algunos casos los porcentajes se pueden calcular mentalmente.

Ejemplo: Hay que calcular el 18 % de 50. Cambiamos de lugar los números y calculamos el 50 % de 18. El resultado es 9. Así que el 18 % de 50 también es 9.

Truco № 2: Contamos los porcentajes como partes iguales

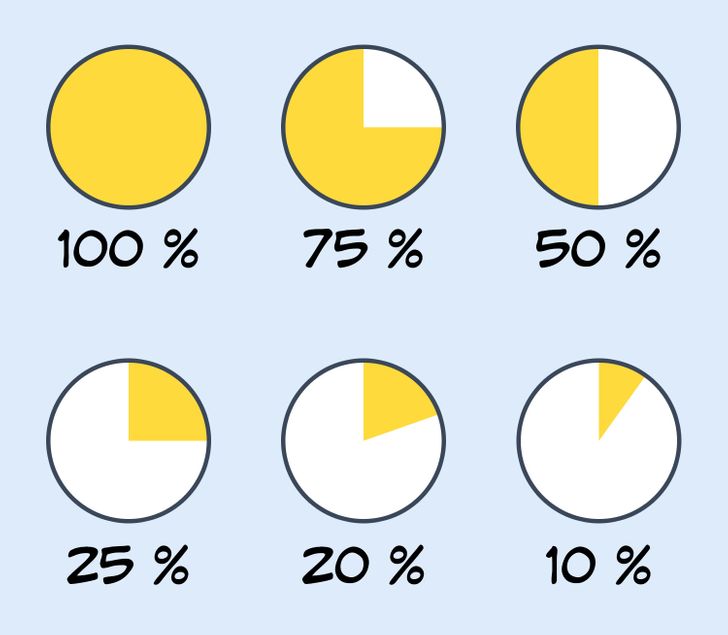
Fíjate en los gráficos circulares de arriba: muestran los porcentajes como partes de un círculo. Por ejemplo, el 50 % ocupa la mitad del círculo, el 25 %, un cuarto y el 20 %, un quinto.

De esta manera, para calcular el 50 % de un número, basta con dividirlo por 2, y para calcular el 20 % de un número, hay que dividirlo por 5. Entonces, siguiendo esta lógica, puedes hacer la siguiente tabla:

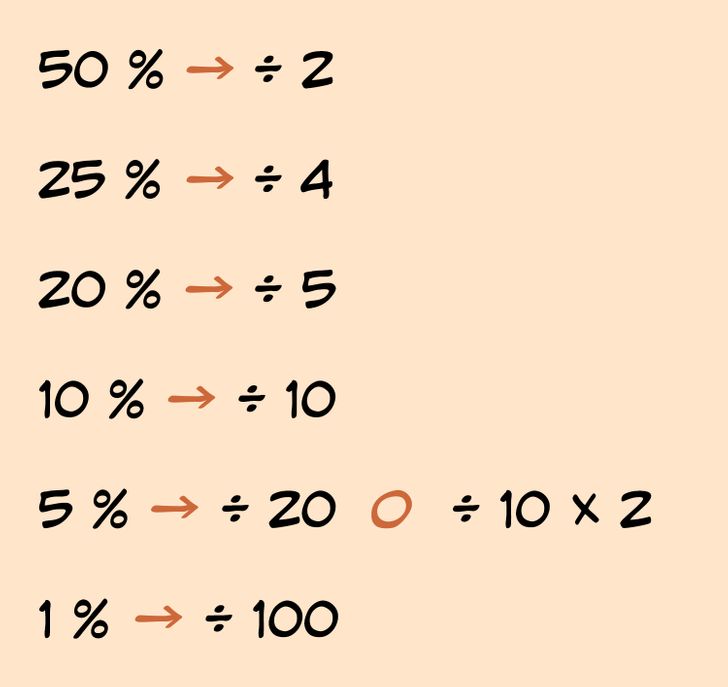
A la derecha de las flechas, se indica por qué número hay que dividir el número (o dividir y luego multiplicar) al calcular un determinado porcentaje de ese número. De esta manera, no tienes que buscar un valor, por ejemplo el 20 %, y luego multiplicarlo por algo, arriesgándote a mezclar números y porcentajes. Basta con realizar una acción.

Los problemas más complejos pueden resolverse de forma similar. Por ejemplo, el 16 % de 42 puede representarse como 10 % + 5 % + 1 %, es decir, 4,2 + 2,1 + 0,42 = 6,72.

Truco № 3: Para resolver todo en una sola acción, mueve los valores

Es sencillo: mueve la coma que separa la parte entera del número de la parte fraccionaria 1 dígito a la izquierda en cada número y luego multiplica esos números. Por ejemplo, para obtener el 90 % de 80, multiplica 9 por 8 para obtener 72. Del mismo modo, para obtener el 21 % de 35, multiplica 2,1 por 3,5 para obtener 7,35.

Ejemplos de problemas de porcentajes en la vida real

Mientras que en la escuela hay que resolver problemas en un cuaderno, en casa las tareas para los niños pueden ser bastante sencillas, pero dirigidas a que aprendan cómo calcular porcentajes en su mente de la manera más fácil posible.

Por ejemplo:

• Para calcular el 10 % de 4 kg, basta con recordar que el 10 % es la décima parte de cien, por lo que puedes dividir 4 kg entre 10. Se obtienen 0,4 kg, es decir, 400 g.
• Para calcular el 5 % de 5 metros, puedes pensar que 5 metros son 500 cm. A continuación, divide 500 entre 10 % para obtener 50. A continuación, divide este resultado por la mitad para obtener el 5 %. Esto significa que el 5 % de 5 metros es 25 cm, es decir, 0,25 metros.
• Para calcular el 40 % de 15 USD, basta con calcular primero el 10 % de 15 USD, que es 1,5 USD, y luego multiplicarlo por 4. Resulta que el 40 % de 15 USD es igual a 6 USD.

Dominar este método ayudará al niño a estar más orientado en la edad adulta, y la capacidad de calcular los porcentajes le permitirá elegir una mejor opción.

Tarea № 1. Dos tiendas en línea venden dos modelos idénticos de auriculares. En la tienda 1, cuestan 45 euros, pero el vendedor promete el envío gratuito a todo el mundo. La tienda número 2 ofrece el mismo precio, pero hace un descuento del 15 %, aunque cobra 8 euros por el envío. ¿Qué tienda es la mejor para comprar los auriculares?

Recordemos que el 15 % es el 10 % + el 5 %. Es fácil calcular que el 10 % de 45 euros son 4,5 euros. Entonces el 5 % son 2,25 euros. Suma 4,5 y 2,25 y tendrás 6,75 euros. Esto significa que el 15 % de 45 euros son 6,75 euros. Por lo tanto, se ahorrarán hasta 6,75 euros al comprar en la tienda № 2, pero al final gastarás más por el envío, que cuesta 8 euros. En este caso, conviene comprar el producto en la tienda número 1.

Tarea № 2. En una tienda hay expuestos unos tenis geniales, con un precio de 260 USD. Y hoy ofrecen un 25 % de descuento extra en toda la mercancía. Solo tienes 200 USD contigo. ¿Tienes suficiente dinero para comprarlos?

Sabemos que el 25 % es una cuarta parte del 100 %. Así que tenemos que averiguar a qué equivale el 75 %, o las tres cuartas partes, del precio en dólares. Para ello, divide el precio sin el descuento por 4 partes y multiplícalo por 3:

260 ÷ 4 = 65

65 × 3 = 195

Resulta que el precio rebajado de los tenis es de 195 USD, lo que significa que definitivamente puedes comprarlos.

Tarea № 3. Has venido a la tienda a comprar un teléfono. El precio es de 376 USD. Te ofrecen adquirirlo con descuento, que es del 11 %, o puedes comprarlo con la tarjeta de la tienda, en ese caso te costará 320 USD. ¿Qué conviene más?

Convierte el 11 % en dinero. Toma el precio del celular y calcula el 1 % moviendo la coma que separa la parte entera del número de la parte fraccionaria 2 dígitos a la izquierda en el número 376. Obtenemos el resultado de que el 1 % es igual a 3,76 USD y el 10 % es igual a 37,6 USD. Suma esto para obtener 41,36 USD.

También se puede calcular de otra manera, utilizando el truco número 3, simplemente desplazando la coma en los números y luego multiplicándolos:

1,1 × 37,6 = 41,36

Ahora resta este número del precio normal del teléfono. Resulta que con el descuento, te costará 334,64 USD, lo que significa que sería mejor utilizar la tarjeta de la tienda y comprar el móvil por 320 USD.