Cómo resolver ecuaciones cuadráticas
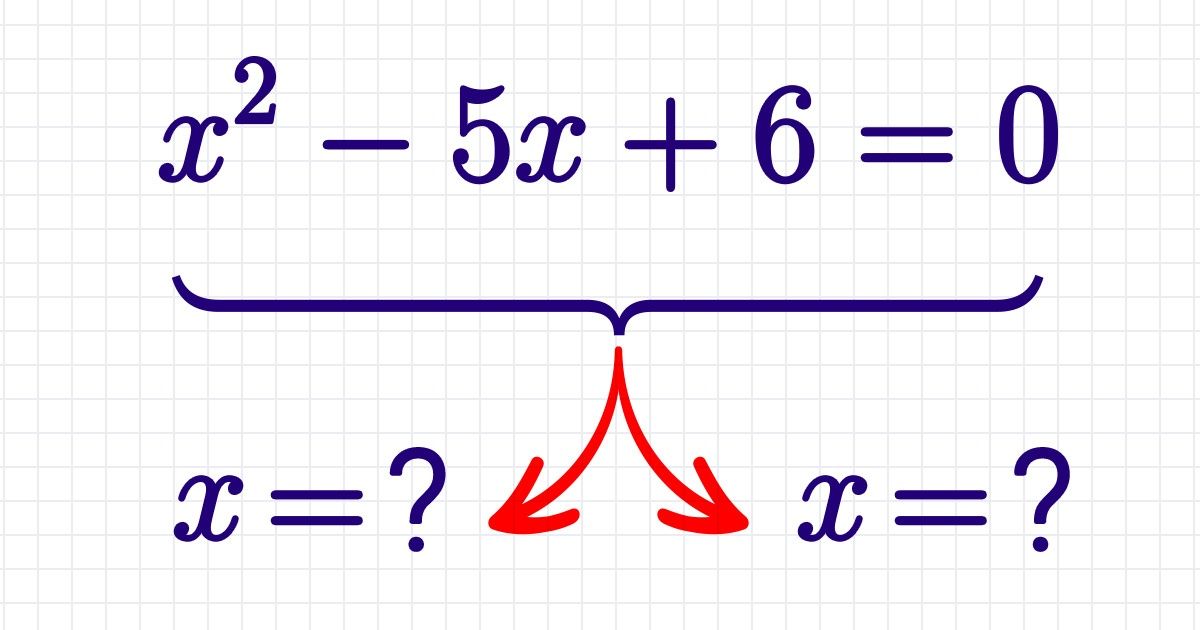
Resolver ecuaciones cuadráticas es un tema importante en el curso de matemáticas de la escuela. Si deseas repasar tus conocimientos, ayudar a tus hijos adolescentes con la tarea o eres nuevo en este tema, utiliza nuestra sencilla guía.
En Ideas en 5 minutos decidimos simplificar este tema tanto como fuera posible para aquellos que tienen dificultades para entender las ecuaciones cuadráticas.
Qué son las ecuaciones cuadráticas

Esta es una ecuación de forma: ax2 + bx + c = 0.
- а — término mayor. También se puede llamar primero.
- b — segundo término.
- c — término independiente.
Practica identificando los términos a, b y c (cuando alguno de estos términos no está presente, es igual a 0).
Ejemplos:
- x2 + 5x = 0. Aquí а = 1, b = 5, c = 0.
- 3×2 + 8x — 7 = 0. Aquí а = 3, b = 8, c = —7.
- —x2 — 3x + 15 = 0. Aquí а = —1, b = —3, c = 15.
- 5×2 = 0. Aquí а = 5, b = 0, c = 0.
- x2 — 5 = 0. Aquí а = 1, b = 0, c = —5.
Cómo resolver una ecuación cuadrática. Paso № 1
Reduce la ecuación a la forma ax2 + bx + c = 0. Solo debe quedar el cero en el lado derecho.
Ejemplo:
- x2 — 3x — 5 = 11 — 3x
x2 — 3x — 5 — 11 + 3x = 0 (las 3x se cancelan)
x2 — 5 — 11 = 0
x2 — 16 = 0
Hemos reducido la ecuación a la forma ax2 + bx + c = 0, donde а = 1, b = 0, c = —16.
Cómo resolver una ecuación cuadrática. Paso № 2
La forma universal de resolver ecuaciones cuadráticas es aplicar la fórmula:
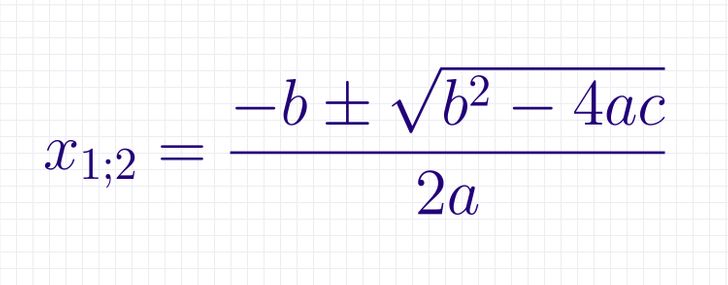
Cualquier ecuación cuadrática se puede resolver con esta fórmula.
A menudo solo se escribe D en lugar de la expresión subordinada b2 — 4ac. D es el discriminante.
Un ejemplo de solución de una ecuación cuadrática usando la fórmula
Comprueba cómo puedes resolver una ecuación cuadrática.
- Anota la ecuación.
- Escribe la fórmula para resolver la ecuación cuadrática.
- Determina los términos. Término mayor а = 1, segundo término b = —5, término independiente c = 6.
- Sustituye a, b y c en la fórmula por 1, —5 y 6.
- Realiza los cálculos.
- Debido al valor positivo del discriminante, la ecuación tiene dos raíces.
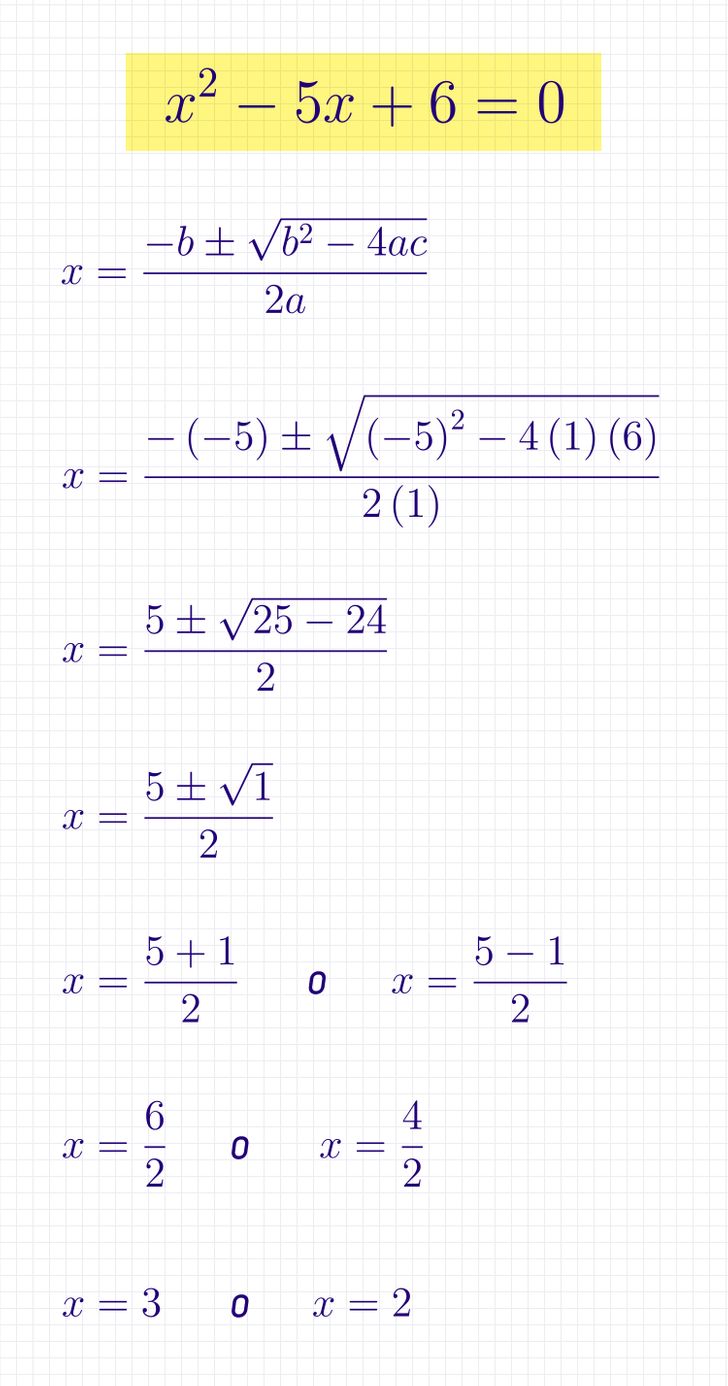
Qué indica el valor del discriminante
Si el discriminante es mayor que 0, entonces la ecuación cuadrática tiene dos raíces o soluciones.
Si el discriminante es igual a 0, entonces la ecuación cuadrática tiene una raíz o solución.
¿Y si el discriminante es menor que 0? Hay una regla: no se puede extraer una raíz cuadrada de un número negativo. Si la solución da como resultado un número negativo bajo el signo de la raíz, la respuesta debe escribirse como “las soluciones o raíces de la ecuación cuadrática no pertenecen a los números reales”.