Qué son los números negativos, cuáles son sus propiedades y qué podemos hacer con ellos

Cuando contamos algo utilizamos los números naturales. Por ejemplo, si cortamos un pedazo de pastel y después otro, tenemos dos trozos. O cuando recogemos manzanas; primero juntamos una y después otra, por lo que en total tenemos dos frutas. Al mismo tiempo, añadimos un número a otro, es decir, utilizamos la suma. Si de manera análoga usamos la resta, entonces en algún momento tendremos un número negativo.

En Ideas en 5 minutos te explicaremos qué son los números negativos, qué propiedades distintivas tienen y qué es útil conocer al trabajar con ellos.

Qué es un número negativo

A primera vista se podría pensar que es poco probable que los números negativos nos sirvan en la vida. Pero solo basta con entrar al elevador de un gran centro comercial y posiblemente ahí verás que los pisos del estacionamiento con frecuencia se encuentran bajo tierra y se demarcan como “-1 piso”, “-2 pisos”, y así sucesivamente.

Incluso los números negativos están en el termómetro de la calle: cuando afuera hace frío y el agua se congela convirtiéndose en hielo, este cae por debajo de la marca 0 °C, lo cual indica que la temperatura es negativa.

Debido a esto podemos concluir que los números negativos comienzan por debajo del cero. Para entenderlo mejor, dibujemos una línea recta.

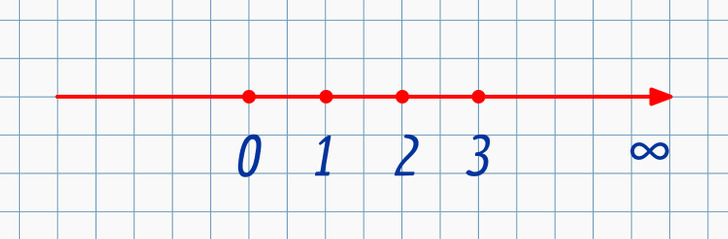
Dibuja una línea en un pedazo de papel cuadriculado. Coloca un punto de referencia para marcar el 0. Ahora deja un espacio de 1 cm a la derecha (2 celdas) y coloca otra marca. Del mismo modo, el resto de los números pueden ubicarse a la derecha hacia el infinito. Todos esos son mayores de 0 y se llaman números positivos. A veces, se suele colocar un signo más al lado de tales cifras, por eso +1 = 1 y 1= +1.

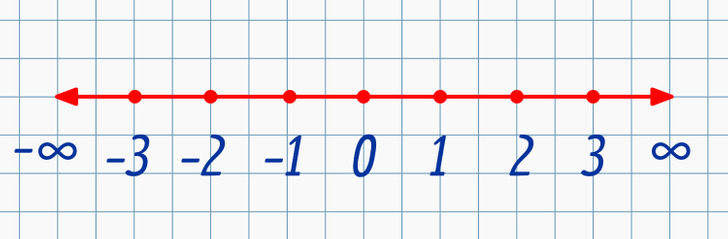
Si nos movemos a la izquierda, entonces veremos a los números que son menores que 0. Por eso se llaman números negativos y se les coloca un signo menos. Al mismo tiempo, −1 es diferente de 1. Los números negativos tienen una posición simétrica con respecto a su par positivo. El 0 no forma parte de los números negativos ni positivos.

Si el cero no es nada, ¿cómo puede existir algo más pequeño que nada? El cero también es un punto de referencia que separa a los números en la recta numérica. En otras palabras, al añadir cifras negativas aumenta la posibilidad de contar. Imagina que una tarjeta bancaria tiene 100 dólares. Después de ir a la tienda su balance es igual a −200 dólares. ¿Cuánto dinero se tendría que agregar a la cuenta para que el balance vuelva a ser positivo e igual a 100 dólares? Si añadimos solo 100 dólares, nos desharemos del número negativo y el saldo será igual a 0. Si agregamos otros 100 dólares, el balance nuevamente regresará a +100 dólares.

Todo eso se vuelve más claro si se observa la línea de números. Para cada número natural existe solo un número negativo, el cual lo complementa hasta cero. Si al número −100 le sumamos +100, obtenemos 0. Si al +100 le restamos −100, el resultado es análogo. De aquí podemos sacar las siguientes conclusiones:

• (−a) + (+a) = 0
• (−a) + 0 = (−a)
• − (−a) = a

Cómo comparar los números negativos

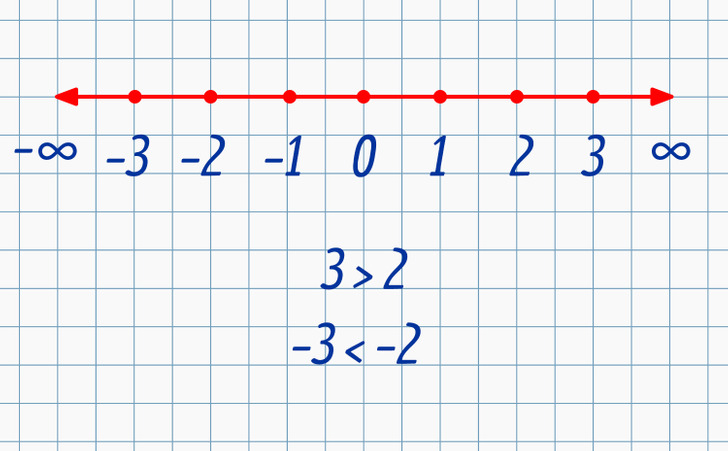
Todos los números negativos, al igual que los positivos, se encuentran en un determinado orden en la recta numérica. Eso permite compararlos entre ellos. Pero existen otras peculiaridades: un número es mayor que otro si se encuentra más a la derecha de este. En otras palabras, el 3 es mayor que el 2 porque está más a la derecha. Con los números negativos, esto es un poco diferente: el −3 es más chico que el −2 porque se encuentra más a la izquierda de la recta numérica.

Operaciones aritméticas con números negativos

Es necesario tomar en cuenta el signo ubicado antes del número, ya que de eso dependerá el resultado.

• Al sumar dos números positivos, como resultado siempre se obtiene uno positivo. Ejemplo: 2 + 3 = 5.
  
• Al sumar dos números negativos, siempre se obtiene uno negativo. Ejemplo: (−2) + (−3) = (−5). Para comprender por qué sucede esto, tienes que recordar la recta numérica: si a −2 le sumamos −3, nos iremos mucho más a la izquierda, a −5.

• Al sumar un número positivo y uno negativo, si el positivo es un número con un valor absoluto mayor, el resultado será un número positivo. Por ejemplo: 5 + (−3) = 2. De hecho, a 5 le restamos 3, por lo cual el resultado es 2.
  
• Al sumar un número positivo y uno negativo, si el negativo es un número con un valor absoluto mayor, el resultado será un número negativo. Por ejemplo: 5 + (−10) = (−5). En realidad le estamos sumando −10 a 5, por eso obtenemos −5.
  

Consejo: posiblemente será más fácil si recuerdas las reglas de los signos después de quitar los paréntesis. Por ejemplo: (+5) + (−3) = 5 − 3 = 2. O (+5) + (−10) = 5 − 10 = (−5).

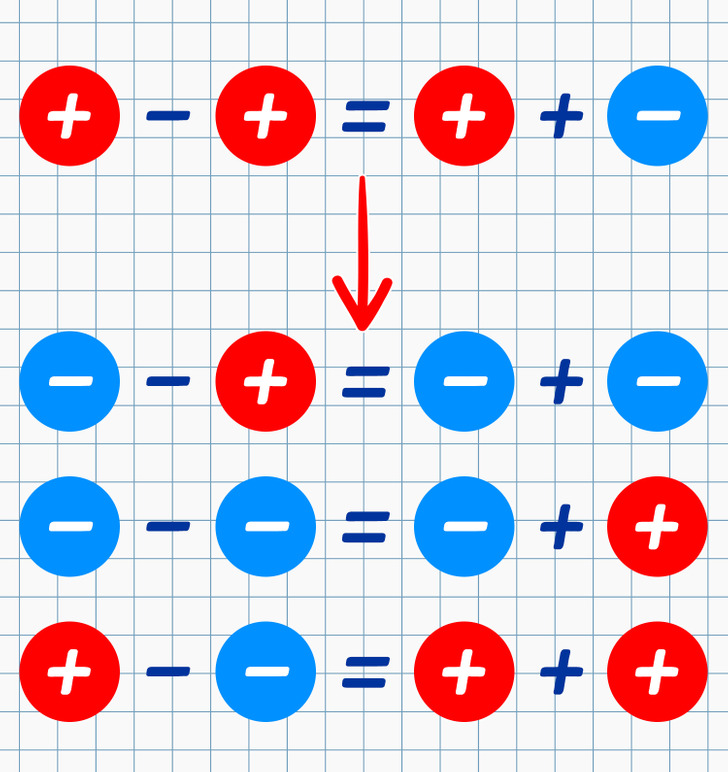
• Como la resta es lo contrario a la suma, entonces para restar un número a otro hay que sumar el número opuesto al que se resta. Por ejemplo: (−2) − (+5) = (−2) + (−5) = (−7). O 5 − (−2) = 5 + (+2) = 7.

¿En qué caso se puede encontrar esto? Imagina que en la calle hace —2 °C y que ahora la temperatura ha bajado otros 10 °C. ¿Qué temperatura hay en la calle? De hecho, se tendría que restar 2 a 10 o sumar —2 a —10. El resultado sería −12 °C.

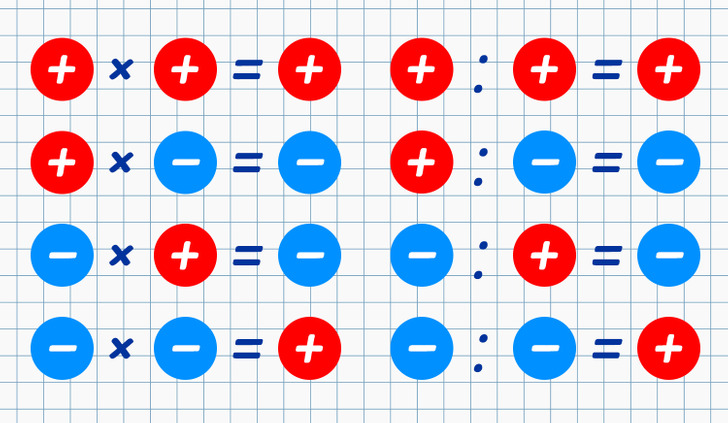
• Al multiplicar y dividir números, se aplica la regla de los signos: el producto o cociente de números con signos diferentes es negativo y con signos idénticos es positivo. Al mismo tiempo, en la división y multiplicación participan los valores absolutos. En otras palabras, (−а) × (−b) = a × b.

¿En qué casos puedes encontrar esto en la práctica? Por ejemplo, un matrimonio se endeuda. Cada uno de ellos tiene una deuda de 100 USD. ¿A qué es igual la deuda común? Para esto tenemos que sumar ambas deudas: (−100) + (−100). O simplemente también podemos multiplicar una deuda por 2: (−100) × 2. Debido a que se trata de una deuda, entonces tendremos que poner el signo menos.

• Si necesitas convertir un número en una potencia negativa, “invierte” la expresión escribiéndola en forma de fracción con un uno en el numerador y el número original en potencia en el denominador. Cambia la potencia por un número positivo y posteriormente convierte este en una potencia positiva. Ejemplo: a⁻ⁿ = 1/aⁿ.