Cómo resolver operaciones con paréntesis

Frecuentemente, el orden de las operaciones matemáticas causa confusión. La situación se complica cuando aparecen paréntesis que no solo pueden dividir una larga expresión en partes, sino también cambiar el orden de las operaciones.

En Ideas en 5 minutos hemos recopilado todo lo que es necesario recordar a la hora de resolver operaciones con paréntesis.

Orden para resolver operaciones sin paréntesis

Para resolver ejercicios sencillos sin paréntesis, calculando raíces y fracciones, es suficiente con recordar la siguiente regla:

• Todas las operaciones se realizan en orden de izquierda a derecha.
• Primero se hacen la multiplicación y la división. Y después, la suma y la resta.

¿Cómo se aplica esto en la práctica?

Ejemplo 1. Calcula el resultado de: 15 − 3 + 7.

Primero realizamos todas las operaciones de izquierda a derecha:

1) 15 — 3 = 12

2) 12 + 7 = 19

La respuesta es: 15 − 3 + 7 = 19

Ejemplo 2. Calcula el resultado de 10 ÷ 2 × 8.

Aquí también realizamos todas las operaciones de izquierda a derecha:

1) 10 ÷ 2 = 5

2) 5 × 8 = 40

La respuesta es: 10 ÷ 2 × 8 = 40.

Ejemplo 3. Calcula: 5 × 4 − 8 ÷ 2.

Aquí también resolvemos de izquierda a derecha, pero hay que tener en cuenta que la multiplicación y la división se realizan primero. Por eso resolvemos de la siguiente forma:

1) 5 × 4 = 20. Esta es la multiplicación y es la operación que se encuentra en primer lugar si nos movemos de izquierda a derecha.

2) 8 ÷ 2 = 4. Esta es la división y tiene prioridad antes de realizar la resta. Por consiguiente, aunque esté más a la derecha, se tiene que resolver después de la multiplicación debido a la prioridad.

3) 20 − 4 = 16. Luego de realizar la multiplicación y la división, procedemos a hacer la resta.

Respuesta correcta: 5 × 4 − 8 ÷ 2 = 16.

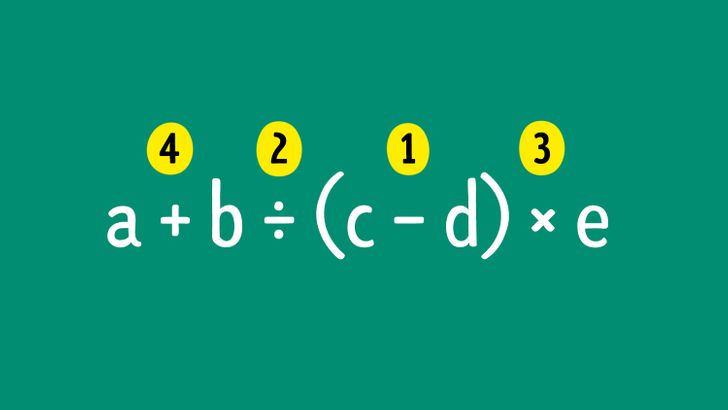
Si la expresión matemática se compone de varias operaciones o si estás aprendiendo su orden, puedes colocar números sobre los signos de las operaciones para determinar el orden en el que deberían resolverse, tal y como se muestra en la imagen superior.

Importante: No es necesario colocar paréntesis cuando se realizan operaciones de suma y resta de izquierda a derecha. Por ejemplo, en lugar de (4 − 2) + 3, es suficiente con escribir 4 − 2 + 3. Tampoco hay necesidad de agregar paréntesis para resaltar las operaciones que tienen prioridad. Por ejemplo, en lugar de 5 + (4 × 3), basta con escribir 5 + 4 × 3, ya que en este caso, la operación de multiplicación tiene prioridad frente a la suma, incluso sin la presencia de paréntesis.

Orden para resolver operaciones con paréntesis

Una expresión matemática puede tener paréntesis. Su función principal es cambiar el orden habitual para resolver las operaciones matemáticas. Recuerda la siguiente regla para no confundirte:

• Primero se tiene que resolver lo que se encuentra entre paréntesis.
• A continuación, realizar las demás operaciones de izquierda a derecha.
• Primero se realizan la multiplicación y la división. Después, la suma y la resta.
• Dentro de los paréntesis se aplica el mismo orden.
• Si una expresión contiene fracciones o potencias, en la medida de lo posible realiza su cálculo antes de resolver la multiplicación o la división, y después pasa a la suma y la resta.

¿Cómo se aplica esto en la práctica?

Ejemplo 1. Calcula: 5 × (8 − 4) ÷ 2.

Siguiendo las reglas mencionadas anteriormente, primero se realizan las operaciones entre paréntesis y después en orden todo el resto. De esta forma obtenemos lo siguiente:

1) 8 − 4 = 4

Al conocer el resultado de la operación entre paréntesis, para una mayor comodidad, podemos escribir en un borrador una expresión como 5 × (8 − 4) ÷ 2 = 5 × 4 ÷ 2. Después resolvemos en orden las operaciones de multiplicación y división:

2) 5 × 4 = 20

3) 20 ÷ 2 = 10

Obtenemos lo siguiente: 5 × (8 − 4) ÷ 2 = 10.

La respuesta es: 5 × (8 − 4) ÷ 2 = 10.

Ejemplo 2. Resuelve y compara los resultados: 7 − 3 + 2 y 7 − (3 + 2).

Calculamos el resultado de la primera expresión: 7 − 3 + 2 = 6. Ahora calculamos el resultado de la segunda expresión: 7 − (3 + 2) = 7 − 5 = 2. La presencia de paréntesis en el segundo ejemplo cambió el orden de las operaciones, por eso el resultado de las dos expresiones es diferente.

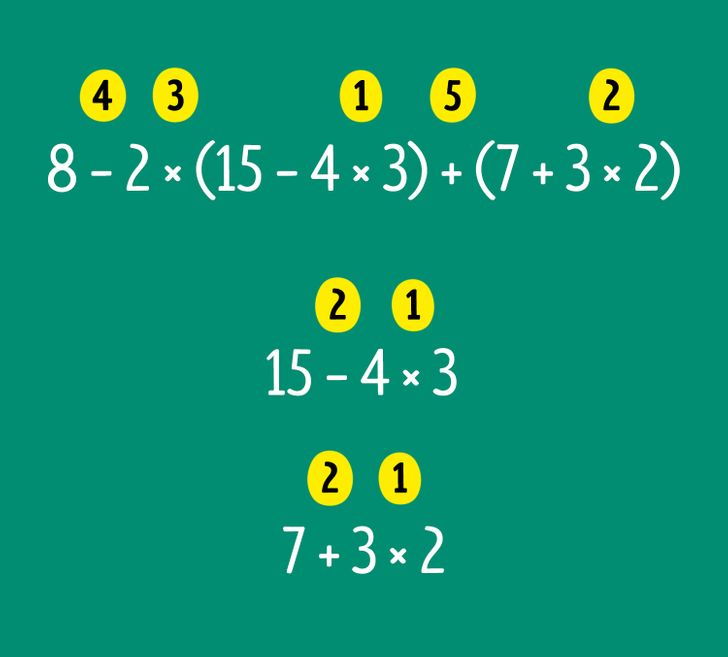
Ejemplo 3. Calcula 8 − 2 × (15 − 4 × 3) + (7 + 3 × 2).

A primera vista, esta expresión matemática parece complicada. Para simplificar el proceso de cálculo, divídelo en pasos separados por orden:

1) Primero resuelve lo que se encuentra entre paréntesis. Para obtener el resultado de la expresión matemática en los primeros paréntesis, hay que recordar qué operaciones tienen prioridad. De esta forma, primero calculamos 4 × 3 y después a 15 le restamos el resultado. La respuesta es 15 — 12 = 3. Continúa con el segundo paréntesis: calcula 3 × 2 y al resultado súmale 7. La respuesta es 7 + 6 = 13.

2) Al saber el resultado de las operaciones entre paréntesis, se puede simplificar la expresión a la siguiente forma: 8 − 2 × 3 + 13. Ahora se debe realizar la multiplicación y después la suma y la resta en orden: 8 − 6 + 13 = 2 + 13 = 15. La respuesta es: 8 − 2 × (15 − 4 × 3) + (7 + 3 × 2) = 15.

Importante: También existen expresiones en las que dentro de los paréntesis hay otros paréntesis. En este caso, la forma de resolver es análoga: primero se debe calcular el resultado de los paréntesis internos, después realizar la operación con los paréntesis externos y al final, lo que está fuera de los paréntesis. Además, el tipo de paréntesis puede variar: los más comunes son ( ), pero también se pueden encontrar { } y [ ].

Errores comunes que hacen que muchas personas resuelvan incorrectamente ejercicios con paréntesis

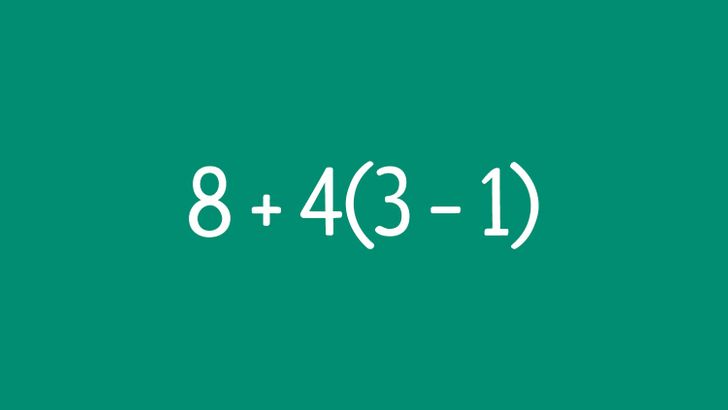
• El signo de multiplicación se omite antes de los paréntesis. Esto puede causar confusión en el orden de las operaciones.

Por ejemplo, calcula el resultado de la siguiente operación: 8 + 4(3 − 1). Al resolver este problema, por error, se podría calcular primero el resultado entre paréntesis, después la resta y al final multiplicar los números obtenidos. Sin embargo, el orden correcto es el siguiente: primero obtenemos el resultado entre paréntesis, después lo multiplicamos por 4 y al final a 8 le sumamos el resultado obtenido. El resultado se vería de la siguiente forma: 8 + 4(3 − 1) = 8 + 4 × (3 − 1) = 8 + 4 × 2 = 8 + 8 = 16.

La expresión matemática 8 ÷ 4(3 − 1) podría verse un poco más difícil. El algoritmo para resolverla es similar. Primero se hacen las operaciones entre paréntesis, después, en orden de izquierda a derecha, se realizan la división y la multiplicación: 8 ÷ 4 × (3 − 1) = 8 ÷ 4 × 2 = 2 × 2 = 4.

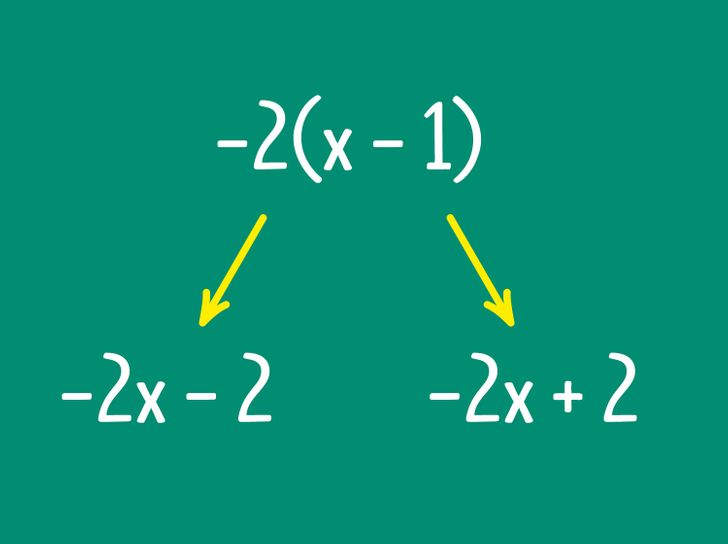
• Ejercicios con paréntesis mal resueltos, en los que al inicio hay un signo menos.

Hay situaciones en las que es necesario abrir lo que hay entre paréntesis para simplificar la expresión. En tal caso, si antes del paréntesis hay un signo menos, entonces al abrir el paréntesis, el signo menos se omite, pero el resto de los signos dentro de los paréntesis se invierte, como si se multiplicara cada número por —1. Por ejemplo, en la expresión 6 + 5 − (4 + 3 − 2), al abrir lo que hay entre paréntesis se convierte en 6 + 5 − 4 − 3 + 2. Los errores más frecuentes se producen cuando hay expresiones con variables y muchas operaciones, por ejemplo: 3 + 2(x + 1) − 2(x − 1). Al no conocer el valor de una variable, no podemos calcular el resultado de la expresión entre paréntesis, por eso es necesario deshacernos de los paréntesis y simplificar la expresión a 3 + 2х + 2 − 2х + 2 = 7. Si no abrimos de forma correcta lo que hay entre paréntesis, entonces podemos obtener lo siguiente: 3 + 2х + 2 − 2х — 2 = 3.

• El cálculo se hace en la calculadora.

No todas las calculadoras son capaces de realizar las operaciones en el orden correcto, aunque hay modelos que están programados para separar las operaciones sencillas de cálculos complejos dentro de una misma expresión matemática. ¿Cómo poner a prueba a tu calculadora? Intenta encontrar el resultado de la expresión 1 + 5 × 7. Si la respuesta es 36, entonces la calculadora puede resolver ejercicios complejos, realizando las operaciones en el orden correcto.