Propiedades de las potencias que serán de ayuda tanto para los escolares como para los adultos

Con frecuencia, en la vida surgen situaciones en las que es provechoso saber elevar un número a una potencia y también resolver problemas tomando en cuenta sus características y propiedades. Por ejemplo, sin estas operaciones no podríamos calcular cuántos azulejos necesitamos comprar para revestir las paredes y el suelo de un baño.

Ideas en 5 minutos te explicará claramente cuáles son las propiedades de las potencias y cuáles son los errores que se cometen con mayor frecuencia al resolver este tipo de expresiones. Guarda este artículo para tenerlo a la mano en el momento necesario.

Qué es la potencia de un número

Cuando multiplicamos un número por sí mismo, denominamos a este proceso elevar un número a una potencia. De esta forma, si multiplicamos la cifra 3 por sí misma, escribimos esto como 3² o “tres a la segunda potencia”.

Para la segunda y tercera potencia, frecuentemente se utilizan nombres especiales:

• Potencia al cuadrado (o potencia de segundo grado), por ejemplo: a²
• Potencia al cubo (o potencia de tercer grado), por ejemplo: a³

Determinar la base de una potencia a partir de su grado o exponente se conoce como obtener una raíz.

Propiedades de las potencias

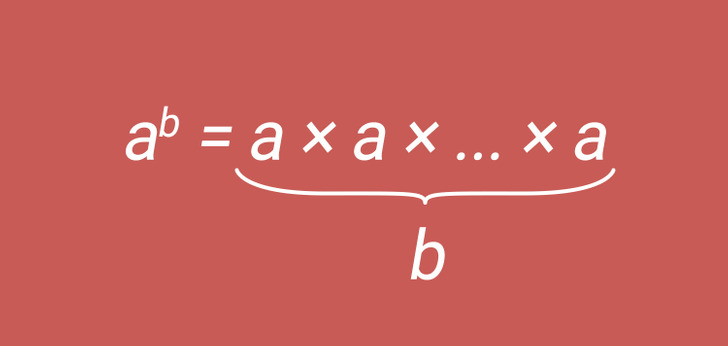
Una potencia tiene una base y un exponente. Mira la imagen superior. La base de la potencia en este caso es a, es decir, el factor que se repite. Y el exponente en este caso es b, es decir, el número de veces que se repite el factor. Esto se lee como “a elevado a la b”.

Si el grado es un número natural, entonces se conoce como exponente natural. De la definición de números naturales, obtenemos que un exponente natural no puede ser cero, un número negativo o una fracción.

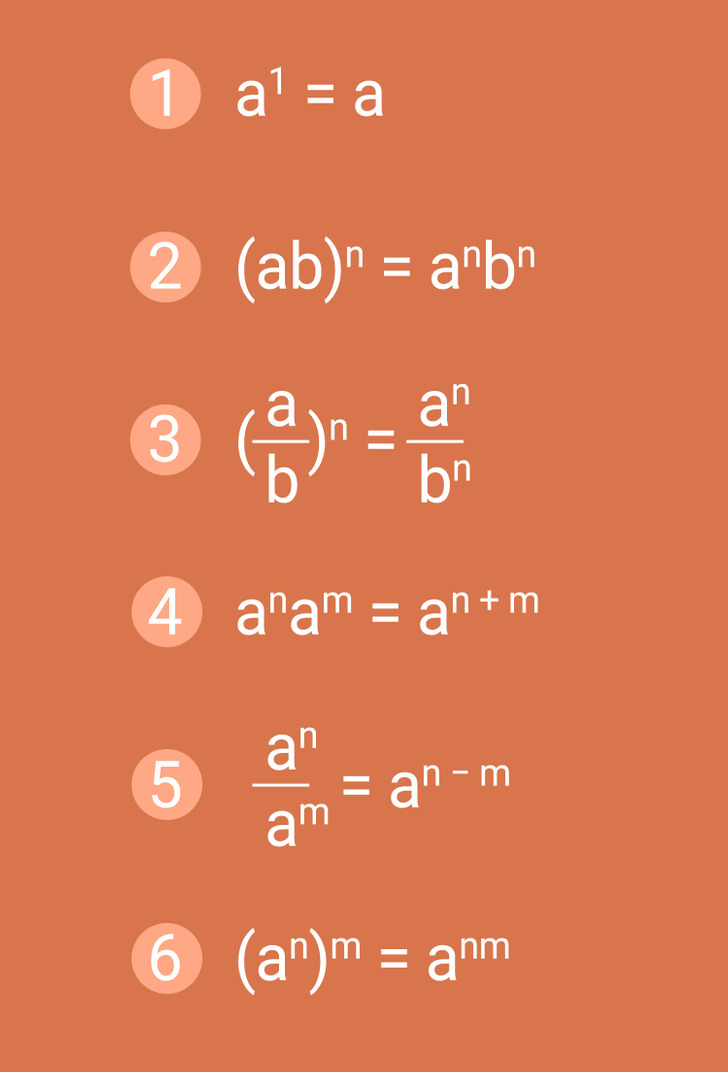
Las potencias con exponentes naturales tienen algunas propiedades que simplifican el proceso de elevar un número a una determinada potencia. Todas esas propiedades están en la imagen superior. Veamos cada una de ellas por separado.

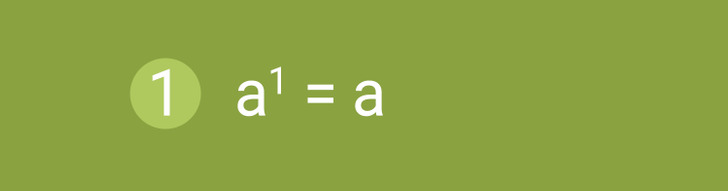
Propiedad 1. Cualquier número se puede elevar a la primera potencia. En este caso, un número elevado a la potencia 1 es igual a sí mismo.

1¹ = 1 y 3¹ = 3. En álgebra generalmente la potencia 1 no se escribe, pero se toma en cuenta cuando se hacen operaciones.

Por ejemplo: a⁴ × a = a⁴ × a¹ = a^{4 + 1} = a⁵.

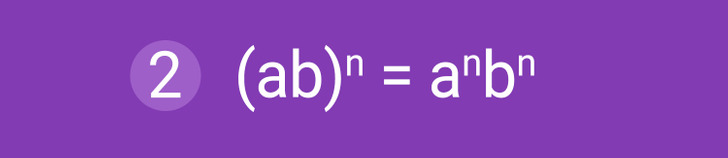
Propiedad 2. Potencia de un producto. Si se necesita elevar el producto de dos factores a una determinada potencia, entonces cada uno de ellos se eleva a dicho exponente y después se multiplica el resultado. Para la fórmula anterior, es necesario que el exponente n sea un número natural.

Ejemplo: (3a)² = (3 × a)² = 3² × a² = 3²a².

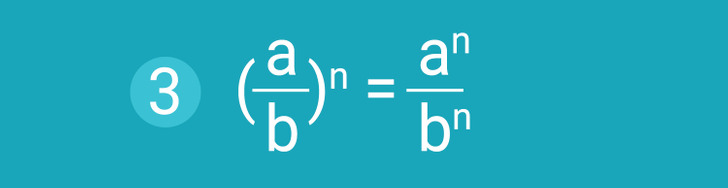
Propiedad 3. Potencia de un cociente. Si se necesita elevar un cociente a una determinada potencia, entonces el numerador y el denominador pueden ser elevados por separado y después se divide el primer resultado por el segundo. Para que este procedimiento funcione, es necesario recordar que b no puede valer 0 y además n tiene que ser un número natural.

Ejemplo: (5/8)² = 5² ÷ 8².

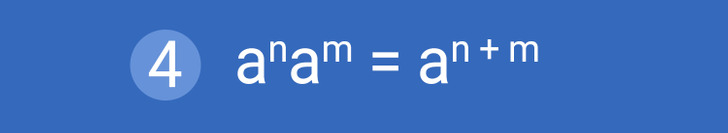
Propiedad 4. Multiplicación de potencias. Si se necesita multiplicar potencias con bases idénticas, se deja la base sin modificar y se suman los exponentes. Para la fórmula anterior, es importante que n y m sean exponentes naturales.

Ejemplo: 3⁴3⁵ = 3⁴ × 3⁵ = 3^{4 + 5} = 3⁹.

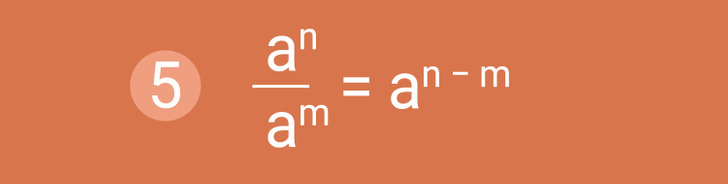
Propiedad 5. Cociente de potencias. Si se necesita dividir potencias con bases iguales, entonces la base queda sin cambios y se resta el exponente del denominador al exponente del numerador. En la fórmula anterior, es importante que a sea cualquier número diferente de cero y que n y m sean cualesquiera números naturales pero que cumplan la siguiente condición: n > m.

Ejemplo: 4⁸ ÷ 4⁵ = 4^{8 − 5} = 4³.

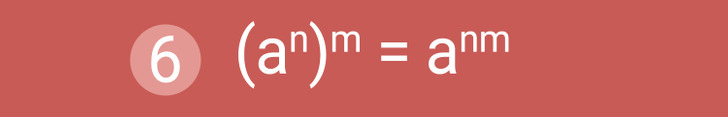
Propiedad 6. Potencia de potencias. Si se necesita elevar una potencia a otra potencia, entonces la base permanece sin cambios y los exponentes se multiplican. En la fórmula anterior, es importante que la base de la potencia sea diferente de cero y n y m, exponentes naturales.

Ejemplo: (4²)³ = 4^{2 × 3} = 4⁶.

Otras propiedades de las potencias

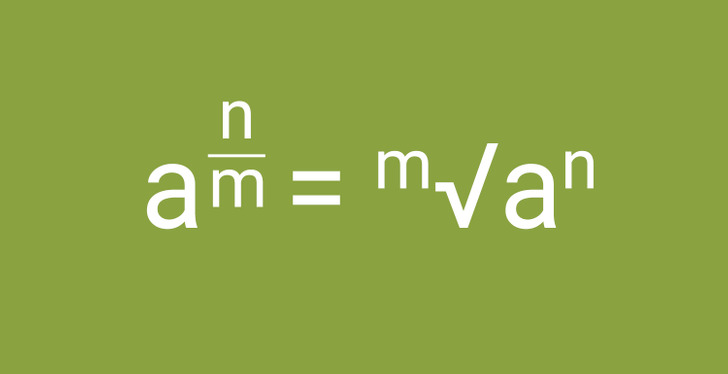
Un número con un exponente fraccionario es igual a una raíz, la potencia a la cual elevamos la base se convierte en el numerador y la raíz se convierte en el denominador. Como resultado, la operación para obtener una raíz siempre se puede reemplazar por una potenciación. Esto se suele emplear para simplificar expresiones.

Ejemplo: ³√a⁶ = a^{6 ÷ 3} = a².

Cualquier número elevado a la potencia cero será igual a 1 (excepto el cero). El cero a la potencia cero da un resultado que en matemática se conoce como “indeterminado”.

Ejemplo: 7⁴ × 7⁻⁴ = 7^{4 + (−4)} = 7⁰ = 1.

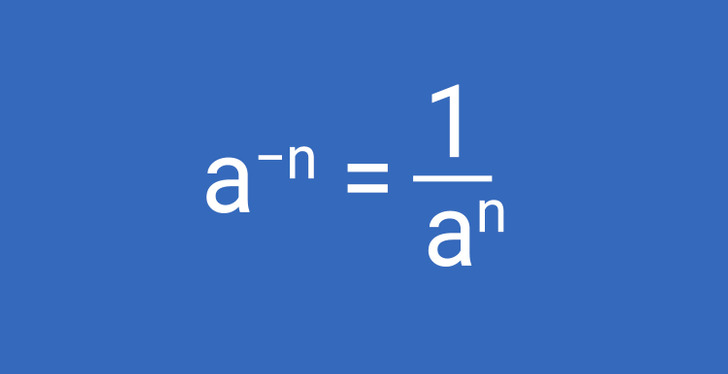
Cualquier número elevado a una potencia negativa es igual a uno dividido por el mismo número, pero con exponente positivo. Si se trata de una fracción, no tenemos más que darla vuelta. En particular:

• a⁻¹ = 1/a
• (a/b)⁻ⁿ = (b/a)ⁿ

Ejemplo: 6⁻² = 1/6² = 1/36.

Una potencia con una base negativa y un exponente par es igual a una potencia con base positiva y el mismo exponente. Para elevar un número negativo a una potencia impar, se debe colocar el signo menos y elevar el número a esa potencia.

Ejemplo: (−8)⁴ = 8⁴ = 8 × 8 × 8 × 8 = 4096. O (−8)³ = −8³ = −512.

Qué errores se cometen con frecuencia en las propiedades de las potencias

• Elevan incorrectamente un número a la potencia cero, a la potencia 1 o a la potencia −1, confundiéndolas entre sí. Tomando en cuenta las propiedades anteriores, recordemos que a⁰ = 1, a¹ = a, a⁻¹ = 1/a.

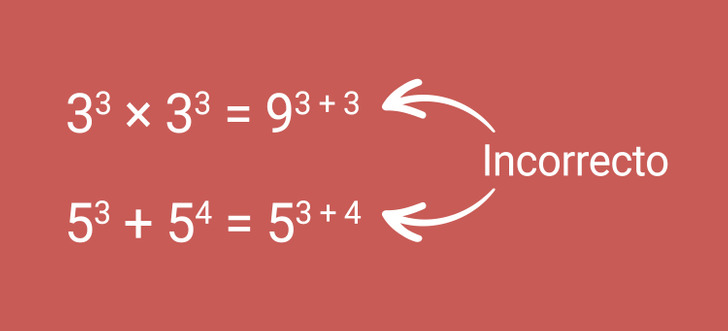
• Multiplican y suman incorrectamente las potencias. Esto ocurre con frecuencia cuando en la expresión de potencias se tienen las mismas bases. Mira la imagen de arriba: en el primer caso las bases no se multiplican, es decir, debería ser 3³ × 3³ = 3^{3 + 3} = 3⁶. En el segundo caso, las bases se están sumando. Por lo tanto, no podemos sumar los exponentes aunque sean iguales. Es necesario elevar cada número a la potencia dada y después realizar la suma: 5³ + 5⁴ = 125 + 625 = 750.

• Elevan incorrectamente un número fraccionario a una potencia negativa. En la imagen anterior, solo la variante inferior coincide con la regla (a/b)⁻ⁿ = (b/a)ⁿ.

Bono: ponte a prueba resolviendo un sencillo ejemplo

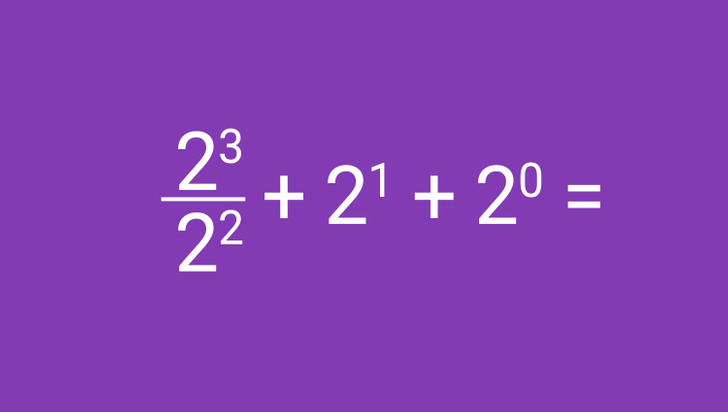
Este ejemplo se ve tan sencillo que parece que hasta un niño puede resolverlo. La realidad es que es capaz de desconcertar a la mayoría de los adultos. Lo más importante es no caer en la trampa y realizar todas las operaciones en el orden correcto. Comencemos por el lado izquierdo y utilicemos la propiedad del cociente de potencias. Tenemos que 2³ / 2² = 2^{3 − 2} = 2¹. Colocamos el resultado en la expresión original y obtenemos 2¹ + 2¹ + 2⁰. En este paso, a algunas personas se les puede ocurrir solamente sumar los exponentes. Pero recuerda que esa no es la manera correcta. Recurrimos a las propiedades para elevar un número a la potencia uno y a la potencia cero. De esta forma obtenemos 2¹ + 2¹ + 2⁰ = 2 + 2 + 1 = 5.

Respuesta: 5.