Tipos de símbolos matemáticos y su uso
Los símbolos matemáticos ayudan a reducir y a simplificar las expresiones matemáticas. Se usan para indicar las operaciones aritméticas, en las comparaciones de los objetos matemáticos, para definir las condiciones de las expresiones o para estructurar otros signos dentro de una fórmula.
Ideas en 5 minutos te muestra qué tipos de símbolos matemáticos hay y cómo se usan correctamente.

🟡 Más ( + ) se utiliza para las operaciones de adición (por ejemplo, 2 + 2).
🟡 Menos ( − ) se utiliza para las operaciones de sustracción (por ejemplo, 4 − 2) o para denotar que un número es negativo (por ejemplo, −2).
🟡 Símbolo de multiplicación ( × ) se utiliza para las operaciones de multiplicación (por ejemplo, 2 × 2). A veces, en vez de este símbolo se usa el punto ( · ) o el asterisco ( * ).
🟡 Símbolo de división ( : ) se utiliza para las operaciones de división (por ejemplo, 4 : 2) o para denotar la correlación entre dos cantidades (por ejemplo, 1:1). Para las operaciones de división, también se puede usar la barra inclinada ( / ).

🟠 El símbolo de igualdad ( = ) se usa para indicar la igualdad (por ejemplo, (5 × 6) = (3 × 10)) o el resultado de las operaciones matemáticas (por ejemplo, 5 + 6 = 11).
🟠 El símbolo de desigualdad ( ≠ ) se usa para indicar que dos objetos matemáticos o partes de expresiones matemáticas no son iguales (por ejemplo, 2 ≠ 3).
🟠 El símbolo de aproximación ( ≈ ) se usa para denotar los valores aproximados y se lee como “aproximadamente igual a” (por ejemplo, π ≈ 3,14).
🟠 El símbolo de equivalencia ( ≡ ) se usa para denotar que una igualdad es verdadera, sin importar el valor de sus variables. Por ejemplo, las partes de la expresión а + (−а) ≡ 0 serán idénticas sin importar el valor de la variable а.
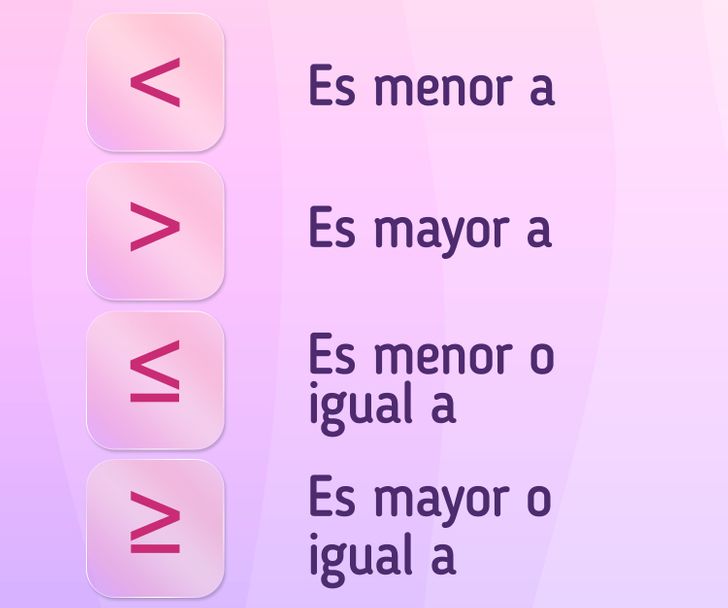
🟣 El símbolo “menor a” ( < ) se usa para denotar una desigualdad, donde un número es menor a otro (por ejemplo, 2 < 3).
🟣 El símbolo “mayor a” ( > ) se usa para denotar una desigualdad, donde un número es mayor a otro (por ejemplo, 3 > 2).
🟣 El símbolo “menor o igual a” ( ≤ ) se usa para denotar una desigualdad donde una parte es menor o igual a otra (por ejemplo, la expresión а ≤ b significa que а < b o a = b).
🟣 El símbolo “mayor o igual a” ( ≥ ) se usa para denotar una desigualdad donde una parte es mayor o igual a otra (por ejemplo, la expresión а ≥ b significa que а > b o a = b).

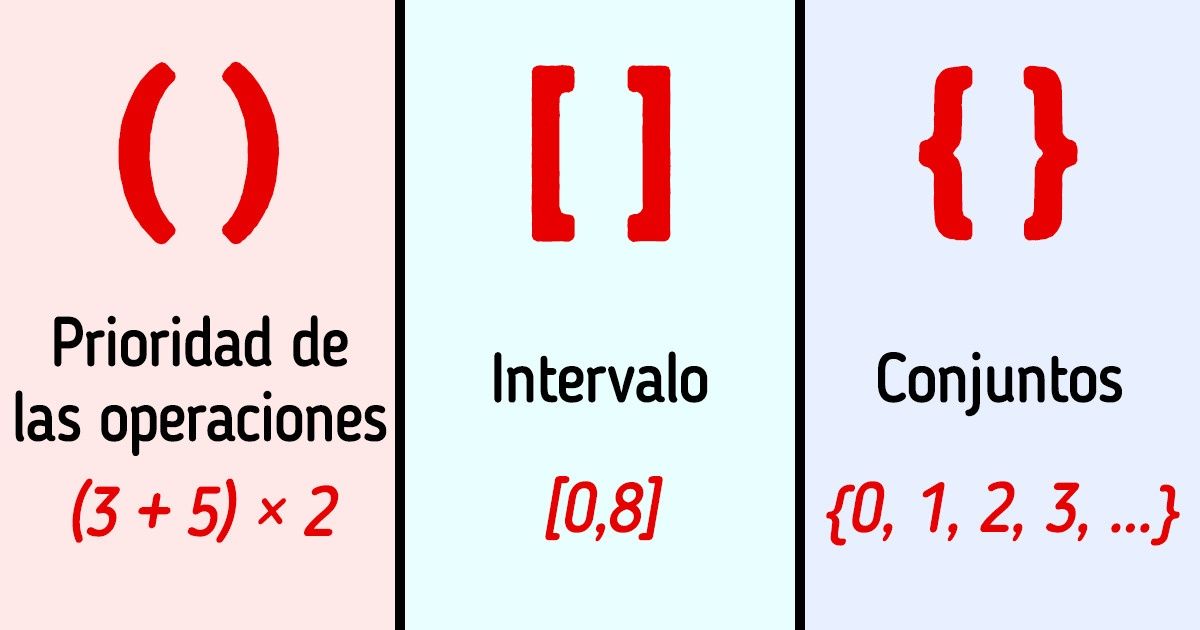
🟢 Los paréntesis ( ) se usan para definir la prioridad de las operaciones matemáticas. Por ejemplo, la expresión (3 + 5) × 2 significa que primero hay que sumar 3 y 5, y luego multiplicar esta suma por 2. Asimismo, los paréntesis se usan para indicar los argumentos de las funciones (por ejemplo, f (x) es la función f, aplicada a la variable x).
🟢 Los corchetes [ ] se usan para indicar la prioridad de las operaciones en calidad de paréntesis de segundo orden. Por ejemplo, la expresión [(3 + 5) × 2]² significa que primero hay que sumar 3 y 5, luego multiplicar la suma por 2, y el resultado hay que elevarlo a la segunda potencia. Además, los corchetes pueden denotar los intervalos. Por ejemplo, [0,8] es el conjunto de números desde el 0 hasta el 8 inclusive.
🟢 Las llaves { } se usan para denotar los conjuntos. Por ejemplo, el conjunto de números naturales {0, 1, 2, 3, ...}.
Otros símbolos matemáticos
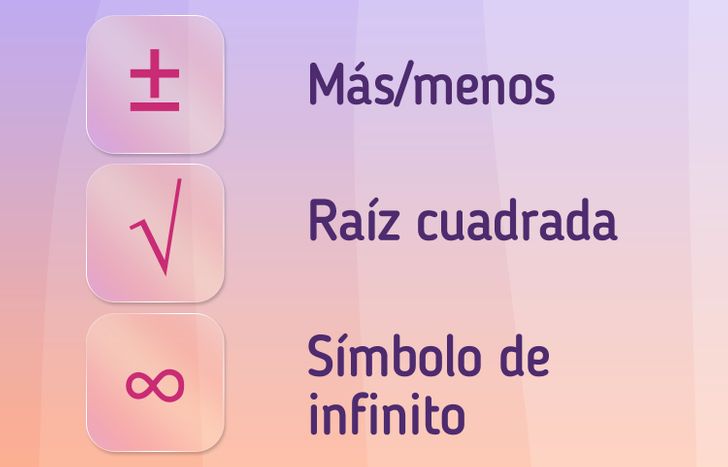
🔵 El símbolo más/menos ( ± ) se usa para indicar el rango de valores. Por ejemplo, 15 ± 3 significa que el valor está entre el 12 y el 18.
🔵 El símbolo de raíz cuadrada ( √ ) denota la raíz cuadrada de un número. Por ejemplo, √4 se lee como “raíz cuadrada de cuatro” y el resultado de esta operación es igual a 2.
🔵 El símbolo de infinito ( ∞ ) significa que el resultado del cálculo no tiene límite. Puede usarse con los símbolos de más y de menos.